Catastrophe Options, traded at the Chicago Board of Trade, and most insurance products provide protection from extreme weather events. Traditional weather insurance can be expensive and requires a demonstration of loss. Weather derivatives are economical in comparison to insurance, require no demonstration of loss and provide protection from the uncertainty in normal weather.
The power industry is facing deregulation around the world. Utilities, unfamiliar with normal cost controls, which are facing unregulated fuel and electricity prices, also anticipate the appearance of competitors appealing to their previously off-limits customer base. Controlling the cost of weather uncertainty may very well be a major tool for utilities to hold onto their customers. For the forward-looking and aggressive utility, it may be a competitive edge with which to gain market share.
While the end-users in the weather market are mostly utilities and insurers, they are merely surfing ahead of the growing swell. Consider the potential of a market that can service the weather risk management needs of three-quarters of the world's firms. This is probably a conservative estimate of those whose earnings are weather sensitive, as almost no one's bottom line is insulated from the fickleness of weather. Moreover, we are in an age of growing corporate awareness of the need for fuller risk management. To these events is added the intense 1996 -1998 El Niņo, whose weather impacts rattled revenues in 1997 and 1998. The confluence of these events has given life to the US weather market; the fledgling market is poised to soar.
Not everybody's weather exposure is the same, and the offsetting weather exposures of different entities will make a robust market. An obvious illustration of an offset is the competing needs of heating gas providers, whose sales rise as outdoor temperatures fall, and their customers who want warm homes and the low heating bills of mild winters. Electricity sellers, whose sales rise as temperatures rise, and who can manage to meet customer's air conditioner cooling needs, benefit in hot summers, while their customers pay less if summer is mild.
Many other opposing weather exposures provide rich opportunities for mutual benefit, if parties can get together. There are, for example, the ski resorts where heavy snowfalls produce revenue windfalls, and local government snow removal agencies whose budgets may be limited. There are the sunshine resorts whose golfers and beach-goers are fair weather customers, and hydroelectric generators who want rain upstream of their dams. There are the take-out pizza chains whose customers become couch potatoes and stay home when weather is extreme, and the restaurants who offer amenities at reasonable prices to entice the same customers to come out when weather is fair. To compile an exhaustive matrix of offsets would be exhausting, although the prospect for market principals and brokers must be exciting.
Power marketers are the prominent market makers. The three principal makers are Koch Industries, Enron Corporation and Aquila Energy. The weather desks at these three companies have taken at least one side of almost all of the estimated six hundred deals that have been done. Other parties in the power industry with regional or national interests, reinsurance companies, and speculators, whose credit is recognized, are potential option sellers. A few direct deals have been done between end-users of options through brokers.
These four interests, power marketers, brokers, energy and reinsurance companies, are present at weather market conferences and are actively seeking transactions. Banks are also present, offering their plans for integrated risk management, and offering to help end-users meet regulatory constraints by transforming deals through their reinsurance subsidiaries. The agricultural community is still quiet about weather derivatives, although they are watching and listening carefully.
Institutional investors, always looking for new asset classes, especially those that are uncorrelated with both interest rates and the equity markets, are waiting in the wings for a secondary market to develop. Slowing the evolution of liquidity are difficulties with the weather data, the scarcity of good weather derivatives pricing models, and confusion over derivatives accounting and regulation issues. The real impediment, however, is the slow acknowledgment by potential end-users of their new ability to manage weather risk.
One aspect of this new market must be appealing to end-users of options, and may be unique: All contracts in the US are tied to objective National Weather Service data. There are no opportunities for disputes over measurements, and there is no way to manipulate the value of the underlying weather for the purpose of gain.
Knowing what to pay for a weather option, however, is another issue. An option's price is keyed to a weather event, not to the price of an underlying security or commodity. The absence of a base that can be traded presents an interesting challenge to option pricing. This is a concern that is frequently discussed among all participants, but is more of a problem for the less sophisticated player.
It is understandable that many enter this market armed with their familiar pricing approaches: either a formulation of a Black-Scholes model or a closed form Asian option model (weather derivatives accumulate over a strike period as discussed in later paragraphs). However, because option prices are not derived from other prices, using these models is wrong, even when they appear to be right.
Nevertheless, most market participants, unprepared to deal with this annoying complexity, and not facing the hazard it presents, proceed incautiously. In the hall outside a weather conference, one broker boasted that his Black-Scholes model yields, from time to time, exact market prices. Another, perhaps more sensible broker, responded sotto voce "A stopped watch is correct twice each day."
Appropriate weather derivatives pricing models are scarce. Some market makers are more advanced in model development than others, and a broker or two seem to have it right, but none have chosen to share the modeling approaches they take. This too is understandable, as it is clear that the competitive edge goes to those with better models. This market-wide paucity of good models presents opportunity for makers, brokers and other players armed with good fair valuation.
The only public discussion of a successful weather option model is by the author of this paper (Dischel, 1998a - see footnote 1). We also discuss the Black-Scholes issues mentioned above and some difficulties with weather data. Our model, which for convenience we can call D1, is a Monte-Carlo simulation of a weather parameter. D1 is the only stochastic model currently available outside the maker-broker circle.
Before we can discuss the D1 model and offer some model results we need to describe a recent real transaction and the option structures found in the current market.
Wisconsin Gas, a subsidiary of the New York Stock Exchange traded firm, WICOR, supplies gas to 525,000 customers in a northern region of the US that borders Canada. Wisconsin depends on heating for 65% of its sales, which is great for them when winter is cold. Nevertheless, in a climate where winter extremes can run 20% warmer or colder than normal, revenue from sales can be volatile.
Curiously, although Wisconsin Gas is a regulated utility, it is not protected by a normalization clause - the kind of clause that permits regulated utilities to share volatility of earnings with customers (and makes them a prime target for competitors in an unregulated market). Wisconsin is long cold winter, and their customers are short cold winter. A cold winter increases the demand for home and office heating and gas sales rise. In a mild winter, Wisconsin's sales shrink in concert with its customers heating bills. Wanting to smooth that portion of its earnings volatility that is weather sensitive, Wisconsin put on a weather hedge.
By structuring a weather collar with El Paso Energy Marketing, a power marketer in Texas, Wisconsin Gas traded a portion of the potential cashflow windfalls of a cold winter for increased cashflow certainty. The collar, to be settled on temperature measurements made at Milwaukee airport at the end of the strike period, was struck at levels that avoided any up-front payments. Wisconsin agreed to pay El Paso if winter was cold, and El Paso agreed to pay Wisconsin if winter was mild. In the partial hedge, Wisconsin Gas held onto some potential upside earnings and gave up some to avoid some of the potential downside of reduced sales. El Paso's interest in executing the collar is less clear.
The 1998 winter was very mild in Wisconsin. Gas sales dipped, but the no-cost collar earned WICOR investors USD 0.04 per share.
The US power industry has found that 65° Fahrenheit (18.3°Celsius) is a convenient temperature for marking the transitions between heating and cooling seasons. This, in turn, led to the concept of degree-days, the accumulation of which over a season, measures the magnitude of the season's demand for heating fuel and electricity for air conditioner cooling. A Fahrenheit degree-day is the difference between a day's average temperature in Fahrenheit (F), and 65°F. For example, if the average temperature on a day is 32°F, then 33 Fahrenheit heating degree-days (HDD) are recorded. If the temperature is 86°F, then 21 Fahrenheit cooling degree-days (CDD) result. The Celsius equivalents of 32°F and 86°F, are 0.0°C and 30.0°C.
Even on the hottest days, there is always some demand for gas, but it is for activities such as cooking not for heating. (See Figure 1. below) As ambient temperatures fall below about 65°F, gas consumption for heating rises with falling temperature. The demand for gas for heating increases more or less proportionally through a range of temperatures, but levels off at a customer's ability to generate heat. Although a customer might prefer to burn more fuel and generate more heat when temperatures are frigid, his physical heating system reaches peak capacity and he cannot: Gas seller revenues are capped.
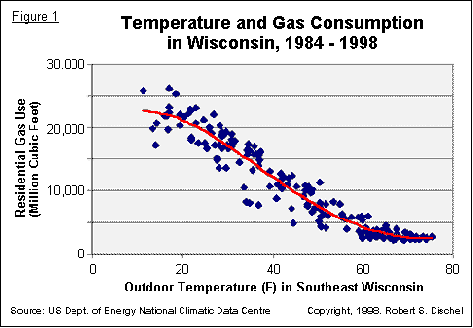
Electricity use is a reverse analogue of the consumption of heating fuel. That is, there is always a need for some electricity, even on the coldest days, for machines and appliances, and for light. The demand for electricity for air conditioner cooling rises as temperatures rise through about 65°F. There is a temperature above which a customer's cooling capacity is saturated and demand for electricity does not rise any higher: Electricity seller revenues are capped.
In the States, even though we call for the comfort of cool rooms in summer and warm homes in winter, we generally size our physical systems region by region. System capacity limitations are encountered only on the most extreme days, meaning that energy suppliers' revenues are probably capped at a higher level in the US than elsewhere.
Market makers originally offered a simple option structure keyed to degree-days to protect the sellers of energy against revenue shortfalls in mild seasons. As all markets do, this one adapted to customer demands, although most of today's deals look very much like the original structures. These current degree-day deals are based on the actual weather measured at the agreed upon US government measurement site, usually the one that is most representative of the weather exposure to be hedged. The degree-day strikes are set not very far off historical means. The degree-days accumulate over a strike period and pay at an agreed upon dollar-per-degree-day rate. Limit strikes are set to cap the option seller's exposure.
For example, when New York City becomes unregulated, a CDD put option could be bought to protect part of the Con Edison's revenues against a mild summer. The contract would be struck to meet Con Ed's needs, but it might look like this: Con Ed pays the seller the agreed upon premium (say USD 300,000) at the time of the agreement. After the strike period, the seller would pay Con Ed for each degree-day below 845 degree-days measured in June, July and August at the National Weather Service site in New York's Central Park up to the limit. Ninety-five percent of the amount due is paid as soon as a preliminary assessment of the accumulated CDDs is known, with any adjustment to the balance paid when the National Weather Service issues the official measure a few weeks later. The payment amount could be set at USD 10,000 per degree-day, with a limit strike of 100 degree-days, capping the seller's exposure at USD 1 million. The average CDD accumulation for the fifty summers (June, July and August) between 1948 and 1997 in New York City's Central Park is 906 degree-days; the standard deviation is 123 degree-days. The attachment strike of 845 degree-days is one-half a standard deviation below the 906 degree-day average. If the CDDs accumulate to a level greater than 845 (a normal to warm summer), Con Ed receives no payment. Figure 2 is the payoff diagram for this put option:

Typical strike periods are whole month increments, although strike periods ranging from one-month to the five month power market season have been done. The meteorological seasons of December - January - February for HDDs and June - July - August for CDDs are the most common.
It has become common for the buyer of the option to specify the attachment strike at any level of his choosing, usually based on his weather exposure, his view on the future season, and the desired level of action. Everyone is concerned about historical degree-day statistics, because the temperature average and standard deviation can be different for different record lengths at a site. Depending on the buyer's and seller's points of view, record lengths of ten to fifty years and longer if available, are used. There are frequent spirited discussions on data and prices.
At-the-money options are uncommon and deep out-of-the-money options have been sold for protection against extreme seasons. Most deals have been somewhat out-of-the money being struck somewhere between one-half and one standard deviation off the site average. Option buyers are often willing to give up only some of their upside for some downside protection.
Many other forms of weather options, such as precipitation and snowfall options, forward year and multi-year deals, and non-linear payoffs are available. All the exotic structures of other option markets have been mentioned.
As in so many markets, a weather derivatives market price is a model price adjusted for a point of view. Pricing uncertainty and difficulties with weather data show up as enormous bid - offer spreads, some exceeding 100% of the bid.
As described earlier, model approaches vary among players, with many mistakenly using Black-Scholes models. The more complex numerical Monte-Carlo models give a more credible measure of fair value, and importantly, calculate a distribution of probable payoffs leading to Value-at-Risk measures.
The author's D1 model is a mean reverting stochastic simulation of the temperature underlying a degree-day option. The model steps forward in time, establishing a new temperature by adding a randomly generated temperature change to an earlier temperature. In this way, the temperature at a location is simulated for a season. Temperature changes from a representative distribution are shaped by the need to revert to the well-understood annual cycle of temperature. Model parameters are optimized for each meteorological site to capture the local statistics. The model is run thousands of times to generate a probability distribution of simulated seasons.
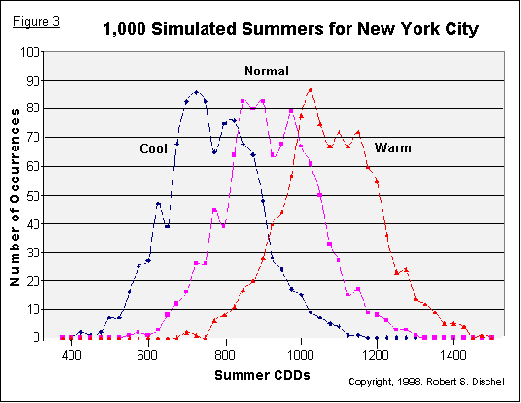
In Figure 3 above, we present the results of three simulations of CDDs for New York City's Central Park summer. The curve in the middle is the primary model result as it is the objective simulation of normal summers. From it, we calculate the expected value of summer CDDs (the average). Counting outcomes inward from the ends of this curve, we calculate the probability of extreme seasons at any desired confidence level. The other two curves are biased distributions: on the left, the distribution is tilted to summers that are cooler than normal, and on the right is the one for summers that are warmer than normal. This is one way to incorporate a view or forecast of a season's outcome, should one hold such a view.
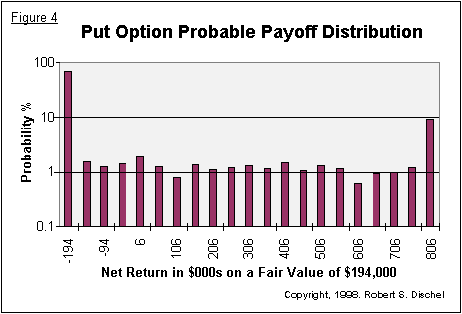
We offer an histogram of the Option Probable Payoff Distribution in Figure 4 below. We used the summer put option in Figure 2 and the model projections of Figure 3 to build the probable distribution in Figure 4. From the data used to build this diagram, we can compute that the fair value of the option is USD 194,000, and we can estimate the Value-at-Risk at any desired confidence level. (We added about 50% to this fair value to get the USD 300,000 option price for Con Edison in the earlier example). Applying the same option structure to the warm and cool summers results in option fair values for these two points of view.
The weather market is struggling with incorporating weather and season forecasts into pricing. For the very reason that there is a weather derivatives market - that weather is uncertain - prices based on forecasts are risky. Nonetheless, the market is vulnerable to forecasts. This fall it was an official US National Weather Service Outlook. The Outlook, based on historical data of La Niņa episodes in the Tropical Pacific Ocean and the average of historical US winters following onset past La Niņa events, suggested a colder than normal winter in the north had an increased probability of occurrence. The market drove up the price of calls on HDDs in the northern US. If the forecast is to be believed, being short northern winter needed to be hedged. An alternative view is that the price impact made the options rich, and presented trading opportunities (Dischel, 1998b - see footnote 2).
Anomalous weather, particularly the devastating rains in California, brought El Niņo into our everyday language and raised our interest in the emerging forecast ability of the meteorological / oceanographic community. Furthermore, we now associate the two extremes of the ENSO cycle (see footnote 3) with impacts on global and US weather. This new awareness also focused attention on the need for hedging weather uncertainty and boosted the weather market, as the forceful El Niņo that began late in 1996 disrupted the weather in the US and upset weather sensitive revenue streams in consecutive 1997 and 1998 seasons.
In the next two parts of this three part series, to be published in future issues of ADT, we will discuss:
- The availability of meteorological data in the US.
- Trends in the data caused by global warming and urban heating.
- Averages, standard deviations and the meteorological record length.
- More results from a mean-reverting stochastic model of temperature.
- El Niņo, La Niņa and other climate events and options pricing.
- Forecast certainty and weather uncertainty.
- Forecasts, nowcasts and hindcasts and their influence on weather derivatives pricing.
Bob Dischel, Ph.D., CCM
Bob Dischel, now a consultant to the weather market, led quantitative activities at two of the US' largest insurers. There he developed measures of risk to portfolios from options and from asset / liability mismatches. Bob was a University Professor and is certified by the American Meteorological Society as a Consulting Meteorologist. He may be contacted at +1 212 799 4256, or by e-mail to bobdischel@worldnet.att.netThis article was submitted to Applied Derivatives Trading on 19 October 1998 and is Copyright 1998, Robert S. Dischel.
Footnotes:
1 Dischel, Robert, 1998a, "Option Pricing - Black-Scholes Won't Do", Weather Risk, A Special Report in the October Issues of RISK and Energy and Power Risk Management.
2 Dischel, Robert, 1998b, "Warning - La Niņa Volatility", November Issue of Energy and Power Risk Management.
3 ENSO stands for El Niņo-Southern Oscillation,
the cycle that we first see in the atmospheric pressure differences along
the Pacific Ocean equator, then in variations in the Pacific Trade Winds,
then in anomalous Pacific sea surface temperatures. El Niņo is the
extremely warm ocean phase, and La Niņa is the extremely cold phase.
El Niņo and La Niņa disturb the "normal" course of the mid-latitude
atmospheric Jet Stream, which in turn shifts weather patterns for the duration
of the anomalous ocean phase.