Ranking the investors in order of yield demanded, we have:
| Investor | Qty. demanded (face value) | Yield demanded |
| 4 | 500,000 | 10% |
| 5 | 300,000 | 12% |
| 2 | 200,000 | 14% |
Let the coupon rate be z%. Then the dollar payments to each investor will be $z the first year and $(100+z) the second year. Discounting these cash flows at the respective yields demanded by the three investors who have won the auction, we can determine the prices paid by them as a function of z. Weighting these prices by the relative quantities demanded by the three investors, we can determine the average price as a function of z. But we know that z must be chosen, so as to ensure an average price of par. This allows us to solve for z.
![]()
Solving, we find that z = 11.37%.
First, we have to see what the land and timber are worth, if not sold. This value depends on how we would deal with the timber and the land, i.e. when would we harvest the timber, when would we sell the land, etc. This is the opportunity cost of the land and timber. The NPV of the purchase proposal mooted by the paper company is then, their purchase price less this opportunity cost.
The timber is currently worth $40 per cord x 1000 cords or $40,000. If the timber is not harvested, this amount increases in value each year at the rate of (1.16)(1.04)-1 for the first 4 years, then at the rate of (1.11)(1.04) for the next 4 years, and at the rate of (1.04)(1.04) for the following 5 years. These values are laid down in row 2 of the table below.
The land value is $100 per acre x 500 acres = $50,000. This amount increases at the rate of 4% per year indefinitely. These amounts are given in row 3.
Row 4 shows the total value of the land and the timber in any year, assuming that the timber has not been harvested upto that point. Keep in mind that the land is not worth keeping, since it grows in value at 4%, while the cost of capital is 9%. The only reason that the land is not sold right away, is that there is no way to sell it without also selling the timber. The timber is certainly not worth selling right away, since it is increasing in value at about a rate of (1.16)(1.04)-1 or 20.64% > 9%. Hence we consider the two as a package. We would also not keep the land and timber after year 9, since at that point, the package increases in value at a rate of 4% at most, while the cost of capital is 9%. The question is, would we keep it as long as year 9, or would we sell it beforehand. From the table below, we see that the value of the land is maximized, in present value terms, if we kept it until year 8. In other words, if we had no purchase offer, we would harvest the timber in year 8, and thereafter sell the land, which action carries a present value of $109,800. The NPV of the purchase offer is, therefore, $140,000 - $109,800 or $30,200.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Future Value | timber | 48.3 | 58.2 | 70.2 | 84.7 | 97.8 | 112.9 | 130.3 | 150.4 | 162.7 |
| land | 52.0 | 54.1 | 56.2 | 58.5 | 60.8 | 63.3 | 65.8 | 68.4 | 71.1 | |
| total | 100.3 | 112.3 | 126.4 | 143.2 | 158.6 | 176.2 | 196.1 | 218.8 | 233.8 | |
| Present value | 92.0 | 94.5 | 97.6 | 101.4 | 103.1 | 105.1 | 107.3 | 109.8 | 107.6 |
a) The profits are $33 per case. The tax rate is 46%. Therefore the net after tax profit per year is 33 x (1-.46) x 1000 = $17,820. Discounting these real cash flows at the real discount rate of (15%-6% = ) 9%, we find that the NPV = 17820/.09 - 150000 = $48,000.
b) We have to consider the fixed and variable costs separately. The PV of the gross margin is [43 x (1-.46) x 1000]/.09 = 258,000, using real cashflows and a real discount rate. The present value of the fixed costs are as follows:
$10,000 nominal dollars a year for ever must be discounted at 15%. This gives us 10000/.15 = $66666.67. However, these costs are deductible. Hence the effective cost on an after-tax basis is only 66666.67 x .54 = 36,000.
This gives us an NPV of -150,000 - 36,000 + 258,000 = $72,000
In part (a), since inflation in both prices and costs is 6%, we can ignore the inflation and just adjust cost of capital to a real rate by subtracting the 6%. In part (b), on the other hand, the inflation is not affecting all costs in the same manner. In this case, we would have to discount the fixed costs separately, using a discount rate of 15%, while all other costs could be computed as real flows and discounted at 15-6=9%. It is clear ex ante, however that the NPV in part (b) should be greater than the NPV in part (a), because in the current year, the total costs at the estimated production level of 1000 units is the same for parts (a) and (b). However, with time, the assumption of a fixed nominal cost of $10,000 will only make the total nominal costs lower in part (b) relative to part (a).
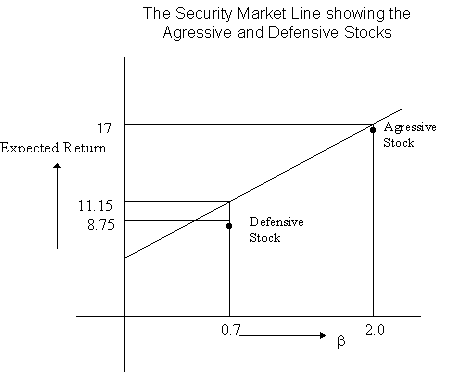
A. If the beta is 0.15, the required rate of return on the bond is .05 + .15(.25-.05) = .08; since investors' horizons are equal to one year, the appropriate riskfree rate is the one year T-bill rate. This means that the 10 year bond should appreciate at the rate of 8% p.a. Hence the price of a 9 year bond next year should be 295 (1.08) = $318.60
B. a. The reduction from 40 to 20 issues should reduce the ability of Hennessy to diversify and would, therefore, increase the risk measured by portfolio variance.
b. Portfolio variance could be reduced by carefully choosing stocks that are not correlated with each other; this may be done by seeking to limit Hennessy's exposure in each industry. However, this would seem to go against Hennessy's mission, which is to find mispriced stocks.
C. Although there may be some advantage in reducing diversification in favor of concentrating on the best stock picks, the marginal disadvantage in terms of such reduced diversification would increase sharply as the number of stocks was reduced. In other words, going from 100 to 90 stocks would increase portfolio variance a lot less than going from 20 to 10 stocks.
D. Obviously, in this case, we don't worry about any individual portfolio's variance, rather we look at the contribution of that portfolio to the overall fund's variance.
E.
a. Let x be the fraction of Dizengoff purchased, and let y be the fraction of Elysee purchased. Then, 30x + 15y = 15. The income from the portfolio is 50x + 50y in the boom state and 20x in the depression state. An individual who is very risk-averse would want to equate the payoffs in the two states. Hence, he would set 50x + 50y = 20x. Solving the two equations, we find that x = 5/7 and y = -3/7 (i.e. 3/7 times the shares outstanding of Elysee are shortsold). This requires an investment of (5/7) x 30 or an investment of $150/7 in Dizengoff, and Elysee is shortsold to the tune of (3/7) x 15 = $45/7.
b. The relevant equations here are 30x + 15y = 15 and 50x + 50y + 5 = 20x. The solutions are x = 11/14 and y = (-4/7). The investment in Dizengoff is $165/7 and Elysee is shortsold to the extent of $60/7.
c. We would conclude that Maureen was willing to take some risk, since the payoffs in the depression state are 20x = $110/7, while the payoffs in the boom state are 50x + 50y = 50(11/14) - 50(4/7) = $75/7, which is different from $110/7.
d. The market portfolio would include all the outstanding shares of Dizengoff, and those of Elysee, as well. This portfolio would have a payoff of $100 in the boom state, and $20 in the depression state. The total amount invested is $30+$15=$45. However, we cannot compute the expected return, because we do not know the likelihood of occurrence of the two states. If, for example, the boom state was likely to occur 1 time in 3, while the depression state was twice as likely to occur, then the expected return would be [(100+2x20)/3]/45 - 1 = 3.7%
e. Maureen, Vitus and Manuel are not as well off, after the merger, as before, because they cannot reach their optimal portfolios. After the merger, they are forced to hold the market portfolio.
To get a better insight into this, consider the distribution of payoffs that are available across states before the merger and after the merger. Normalize the payoffs to securities by converting them into returns. Then we have:
| Net returns in both states of the world | ||
| Boom | Depression | |
| Dizengoff | 2/3 | -1/3 |
| Elysee | 7/3 | -1 |
| Market | 11/9 | -5/9 |
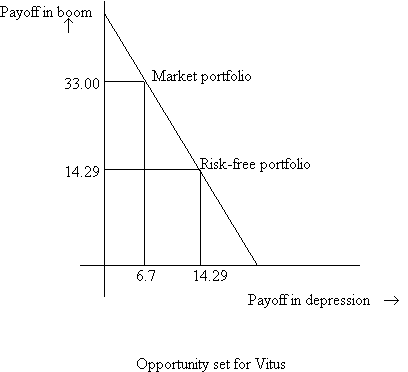
Plotting this on a graph with net returns in the two states on the two axes, we have:

Starting with points D and E, we can combine them to obtain M (the market portfolio) and F, the portfolio that has returns equal in the two states. After the merger, only point M is available. Hence the opportunity set of the investors has shrunk tremendously.
f. If riskless borrowing and lending were permitted, then Maureen, Vitus and Manuel could combine riskless borrowing and lending with trading in the market portfolio to reach their optimal portfolios from before. Again, refer to the graph above, with D and E, both M and F are accessible. However, we only need 2 points on the line to generate the entire line. If E and D merge, we can still generate the entire line, as long as F is also available.
Computation of the riskfree rate:
We see from part a. that the riskless portfolio could be recreated by holding 5/7 of Dizengoff and shortselling 3/7th of Elysee. This would yield a payoff of 20x = 50x + 50y = 20(5/7) = $100/7 in both states, for an investment of $15 up front. This implies a rate of return of (100/7 - 15)/15 = -4.76%.
What are the state prices, i.e. the attributable market price to a dollar of earnings in the boom state, and in the recession state?
We know that 50x + 20y = 30, and 50x = 15. Solving the equations, we see that x = 0.3, and y = 0.75. A security paying $1 in the boom state and nothing otherwise would sell today for 30 cents, while a security paying $1 in the depression state and nothing otherwise would sell today for 75 cents. Consequently, in order to be sure of getting $1 next period, one must invest $1.05, implying that the riskfree rate of interest is 1/1.05 - 1 or -4.76% as derived earlier.