• Spring 1994, Midterm, Rutgers University
• Solutions to Spring 1994, Midterm, Rutgers University
• Spring 1994, Final, Rutgers University
• Solutions to Spring 1994, Final, Rutgers University
• Spring 1993, Midterm, Rutgers University
• Solutions to Spring 1993, Midterm, Rutgers University
• Fall 1993 Final, Rutgers University
• Solutions to Selected Problems from Fall 1993 Final, Rutgers University
• Summer 1993, Midterm, Rutgers University

• 1. Explain all your steps.
• 2. Show all your computations.
• 3. Write legibly; I cannot guarantee any points for what I cannot read, even if it is correct.
• 4. If your approach is correct, you will get some points, even if your arithmetic answer is wrong. So concentrate on getting your logic right.

1. Johnny Appleseed is a mean variance optimizer with a risk aversion coefficient of 3. For the coming year, he has the choice of investing his nest egg of $2000 in one of two risky mutual funds, A and B. In addition to being able to invest in one of funds A and B, he can also invest in a short-term money market fund that invests in U.S. Treasury bills, which yield 6% currently. The money market fund also allows good clients like Johnny to short sell the money market fund with minimial transactions costs. The following additional information is available on the two funds.

Mutual fund	E(r)
A	9%	20%
B	10%	25%

a. Which mutual fund should he choose? (20 points)

b. If Johnny were required to swap from his preferred fund to the less preferred fund in exchange for an upfront payment, what is the minimum that he would demand? (10 points)

(Point of information: if, for whatever reason, Johnny was denied the opportunity to invest in his preferred fund, the payment computed in part b. would be a measure of the loss that he would suffer.)

2. a. Merrillynch Funds advertises that they have beaten the market three out of every four years. How could they achieve such a result if markets are efficient? (10 points)

b. Suppose now, that a team of Rutgers professors investigates Merrillynch's portfolio returns over time, and concludes that their investment strategy is, in fact, capable of generating abnormal returns. Simultaneously, it becomes known that Merrillynch has access to supercomputers that are able to detect patterns in stock prices before anybody else can. This latter piece of news obviously buttresses the findings of the finance professors from Rutgers. Should you invest in Merrillynch stock? (10 points)

3. Suppose you can buy a call option on Telefonos Mexicanos (Telmex) for $1, with an exercise price of $28, and a time to expiry of 3 months. The stock is currently selling at $25.

a. Assuming that the option is American (i.e. it can be exercised before maturity), would you exercise the option now? (5 points)

b. Now assume that the option is European (i.e. it cannot be exercised before maturity). The following information is available to you about the holding period returns over the following three months (non-annualized).

i. What is the beta of Telmex stock? (5 points)

ii. What is the beta of the call option on Telmex? (5 points)

iii. Do the stock and option prices satisfy the Capital Asset Pricing model? If you believed in the CAPM, what strategy would you employ? (15 points)

4. You have two jobs waiting for you when you get your Rutgers MBA--one at United Technologies, and the other at General MacIntosh Corporation. The following information on the price performance of both companies' stocks is available to you.

Company	E(ri)	i
United	28%	49.03%
GMC	32.5%	60.21%
Market portfolio	25%	40%
Zero-beta portfolio	10%	50%

i. Assuming that the CAPM holds, and that the single index model describes security returns, what is the security specific risk of each company's stock? (15 points)

ii. If working conditions, salary, etc; were comparable at the two companies, which company should you prefer from a portfolio theory perspective? Why? (5 points)

Alternate question

3. If the variance of market returns increases by 50%, what would you expect will happen to expected returns, assuming that the average degree of risk-aversion remains constant? Answer concisely. (15 points)

Solutions

1. a. The capital market line has slope (9-6)/20 = .15 for A and (10-6)/25 = .16 for B; so B is better.

b. We need to find out the investor's utility if B is chosen versus if A is chosen. The difference is the upfront payment required.

To begin, we need to compute the optimal proportion to invest in both funds. This is given by the formula y* = [E(r_p)-r_f]/(.01A_p²). This gives y_A = 0.25, while y_B = 0.2133.

E(r_pA) = 6.75%; _pA = 5%; E(r_pB) = 6.8532%; _pB = 5.3325.

Using this, we can compute the certainty equivalent of the two portfolio returns by using the utility function: U(r) = E(r)-0.005A². This gives 6.375 for A and 6.4267 for B, or a difference of 0.051667%. With an initial investment of $2000, this works out to a $1.03 difference in terminal portfolio value (certainty equivalents). Using the riskfree rate to discount this to the present, we get an upfront payment required of 97.48 cents.

2. If Merrillynch held a high beta portfolio, they could achieve higher than average returns more frequently, even if markets were efficient; provided markets were sufficiently variable, and the market risk premium were sufficiently large.

Suppose all returns are distributed normally. Further, let the CAPM hold, so that E(rp) is given by r_f + _p(E(r_m)-r_f). Let the market risk premium be high, say 6%. Then, if E(r_m) = 10%, a portfolio with a beta of 2 would have an expected return of 20%. Assuming performance each year is independent, in order to beat the market 3 times out of 4 on average, the probability p of beating the market in any one year is given by 0.75. Hence, we want Pr{r_p>r_m} = Pr{r_p-r_m} = 0.75, which requires E(r_p)-E(r_m) > 0.675 s.d.(r_p-r_m).

Using an index model, var(r_p-r_m) = (_p-1)2var(r_m) + var(_p) = var(r_m) + var(_p). Hence the condition boils down to var(r_m) + var(_p) < 219.48. If var(_p) were zero (the fund chose a diversified portfolio), this requires the market std. devn. to be no more than 14%, which is not impossible.

3. a. Since it is out of the money, it would be irrational to buy it now.

b. The beta of a security is the ratio Cov(r_m,r_s)/Var(r_m). Using the formula

Var(r) = E(r-E(r))², we can compute var(r_m ) as

E(r_m) = (25+5-15)/3 = 5; E(r_tel) = (30+15)/3 = 15

var(r_m) = 800/3 = 266.67; Cov(r_m,r_tel) = 600/3 = 200. Hence, tel = 200/266.67 = 0.75.

E(r_option) = (350-25-100)/3 = 75; Cov(r_option,r_m) = (275*20+175*20)/3=3000; opt = 11.25

Assume the stock is properly priced (according to the CAPM);

then E(r_tel) = rf + 0.75(E(r_m)-rf), which implies that rf = 45% > E(r_m) = 5%! Hence the stock is mispriced. If the option were properly priced, then the interest rate would be -1.83% < 0; hence the option is also mispriced. However, clearly, the stock is underpriced relative to the market, while the option is overpriced.

Relative to each other, which is overpriced, and which underpriced? This depends on the actual risk free rate. If the two securities were priced correctly relative to each other, we would have . This implies that r_f = 10.71%. If r_f > 10.71, E(r_opt) = 75 > r_f + 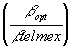[E(r_telmex)-r_f) and the option would be underpriced relative to the stock; we could then buy the option and short the stock; however, we must be careful to buy the right amounts. For example, if r_f = 12%, we would short sell the stock for 15 (11.25/0.75) times as many dollars, as we would spend on options. This would make the beta of the combined position zero (the portfolio weights would be -15/14 in stocks, and 1/14 in the option, which would give us a net borrowing position. The return on this is (-15/14)*15 + (1/14)*75 = -10.71%; in other words, we are borrowing at 10.71%. We now lend this out at 12% and make a bundle. If r_f < 10.71, the stock would be underpriced relative to the option, and we would take the opposite position.

4. i. Assuming the CAPM holds, we can compute each firm's .

E(r_i) = E(r_z) + _i[E(r_m)-E(r_z)

_United  = (28-10)/(25-10) = 18/15 = 1.2

_GMC = (32.5-10)/(25-10) = 1.5

From the single-index model, we know that Var(r_i) = 2 Var(r_M) + Var(i).

Hence, Var(United) = 100; Var(GMC) = 25

ii. Since a lot of one's wealth is human capital, which is usually very difficult to sell shares in (non-marketable), and since there are restrictions on shortselling (at the very least, it is costly), the individual's portfolio is likely to be non-diversified; hence it could be argued, on portfolio theory grounds, that a firm with less diversifiable risk (firm/asset specific risk) is preferable, so that the individual's portfolio will also have less diversifiable risk (which is not compensated for, by the market).

• Explain all your steps; correct answers without explanations may not be given any points at all.
• Show all your computations and formulae. Make all your assumptions explicit. If your approach is correct, you will get some points, even if your arithmetic answer is wrong. So concentrate on getting your logic right.
• Write legibly; I cannot guarantee any points for what I cannot read, even if it is correct.

1. The following are average yields on U.S. Treasury bonds at two different times.

a. Assuming that the above bonds are zero coupon bonds, calculate the forward rate for a three-year U.S. Treasury zero-coupon bond two years from May 15, 19XX. (10 points)

b. Assuming that the above bonds are coupon bonds selling at par, describe a procedure that would enable you to determine the forward rate for a three-year U.S. Treasury zero- coupon bond two years from May 15, 19XX. What other information do you require, if any? (10 points)

c. i. Discuss how the Unbiased Expectations Hypothesis could explain the January 15, 19XX term structure shown above. (5 points)

c. ii. Discuss how the Liquidity Premium Hypothesis could explain the January 15, 19XX term structure shown above. (5 points)

d. How might you explain the change in the term structure from January to May? (10 points)

2. Riding the yield curve is an active bond portfolio management strategy that can be described as follows:

Assuming an upward sloping term structure, buy securities with somewhat longer term to maturity than desired, and then sell them before they mature, thereby capturing some capital gains.

Give an example of this with zero coupon securities, and explain the disadvantages of this strategy, if any. (Note: This question can be answered using solely the concepts discussed in class.) (20 points)

3. The yield curve on zero-coupon U.S. Treasury obligations is shown below:

You are the financial vice-president for a casualty insurance firm and have estimated that the firm will have to pay $7 million in damage claims in exactly 2 years and $10 million in exactly 3 years.

i. If you were to place some of your money in 2 year and 3 year zero-coupon bonds today, what percentage should each represent in order to be fully immunized? (10 points)

ii. If you were to place some of your money in 1 year and 4 year zero-coupon bonds today, what percentage should each represent in order to create an asset portfolio with the same duration as that of your liabilities? Will the resulting portfolio of assets and liabilities be immunized against parallel term structure changes? Explain your answer clearly and fully. (15 points)

iii. Assuming that the term structure moves up by 1% at all maturities, which of the immunized portfolios of assets and liabilities in i. and ii. will have a higher value after the yield change? No credit without explanation. (15 points)

Solutions:

1.a. The forward rate is given by: (1+f)3 = (1.077)5/(1.079)2, or f = 7.56%.

b. Solve a set of linear equations of the form P = _iC_id_i where i indexes the time of the flow. The resulting i's can be used to generate the yields on zero coupon bonds. The coupon rate is known because all the bonds are assumed to be selling at par. However, we do not have information on the yields on 3- and 4- year bonds (assuming coupons are paid annually; otherwise yields on other bonds--1/2 yr, 1 1/2 yr. etc; will be reqd.). Alternatively, we can estimate the required forward rate by applying regression techniques to the available bond data.

c.i. The upward sloping nature of the term structure on Jan. 15 is due to the market's expectations that interest rates will gradually increase.

c. ii. The upward sloping nature of the term structure on Jan. 15 is due to an upward sloping liquidity premium structure.

d. The market's expectations regarding future interest rate behavior changed.

2. The problem with this is that the shape of the term structure could change, such that the expected capital gains may never materialize.

3. i. 7/(1.1)² vs. 10/(1.11)³, or 5.785m. vs. 7.312m. or 44.17 vs. 55.83%.

ii. The duration of the liability portfolio is .5583(3) + .4417(2) = 2.5583.

If x is the proportion placed in 1 year bonds, we have x + (1-x)4 = 2.5583, which solves to x=.4806. This portfolio will immunize the liabilities, because the dispersion is greater than that of the liabilities.

iii. The portfolio immunized by 2 year and 3 year bonds will not change in value at all. Since the portfolio immunized by 3 and 4 year bonds is immunized and it is not perfectly immunized, it must have an increase in value, because of convexity.

• ..Make all your assumptions explicit.
• ..Show all steps and please write legibly.
• ..Show all formulae clearly.

1. (20 points) Suppose you have $10,000 to invest and would like to sell $5,000 in stock B short to invest in stock A. Assume that the covariance between the returns on stocks A and B is zero. Calculate the expected rate of return and standard deviation.

Stock	A	B
E(r)	.12	.02
(r)	.08	.10

2. (20 points) If the variance of market returns increases by 50%, what would you expect will happen to expected returns, assuming that the average degree of risk-aversion remains constant? Answer concisely.

3. (30 points) An investor is faced with the problem of finding the efficient portfolio with an expected return of 8% when the market consists of two risky assets with the following characteristics:

Covariance between r₁ and r₂ = .0003

The return available on the riskless asset is r = 5%. Find the corresponding efficient portfolio consisting of the riskless and the risky assets. Does the investor borrow or lend at the riskless rate?

4. (30 points) If you were a specialist for XYZ Corp. and saw that there were a large number of limit orders to buy at $12, how would you adjust your inventory if current trading was at 12 1/4? Why?

Solutions:

1. w_A = (15/10) = 1.5, while w_B = (-5/10) = -.5

E(r_p) = (1.5)(.12) - (.5) (.02) = .17 or 17%

_p = (1.5)2(.08)2 + (.5)2(.1)2 = .0169; p = .13

2. E(r_m) - rf = (Average A) x .01 x _m

Hence, if _m increases by 50%, all excess returns increase by 50%. This assumes that the relative investments in the riskfree asset and the riskless asset don't change the relative returns directly. It is possible that the increase in volatility will increase the riskfree rate because of an increase in desire to hold riskfree assets relative to risky assets.

3. Applying the formula given by eqn. (7.8) on p. 211 of Bodie, Kane and Marcus (2nd ed.), we have w₁ = 3.33, w₂ = -2.33.

This creates a tangent portfolio with an E(r_p) = 3.33 (.06) - 2.33(.10) = -.0333

The final portfolio must have an expected return on 8%. Hence if is the proportion in the riskfree asset, must satisfy .08 = (.05) + (1-)(-.0333), or = 1.36; i.e. he shortsells the risky tangent portfolio for 36%.

4. I would increase my inventory, because the knowledge that there were many limit orders to buy at $12 gives me a floor price to dispose of my inventory.

• All questions are equally weighted.
• No points will be given for answers without explanations.

1. (25 points) Here is a news item from The New York Times of October 5, 1993:

Shares of Metricom Inc. surged 28.6 percent after Paul Allen, co-founder of the Microsoft Corporation, bought a 13 percent stake in the company. Mr. Allen's investment company, Vulcan Ventures, Inc., based in Seattle, purchased 1.17 million of Metricom's common shares for $17.5 million and acquired 408,333 warrants to buy the compnay's stock at $20 a share. Shares of Metricom rose $4.50, to $20.25, in Nasdaq trading.

Mr. Allen, a billionaire who still has a substantial stake in Microsoft, is known for backing interactive-information ventures. Metricom is a developer of a high-performance wireless data communicaitons network that is currently in the testing stages. In the second quarter, Metricom posted a loss of $1.6 million on revenue of $1.6 million.

a. Does this refute market efficiency? Why or why not?

b. Does this refute the CAPM, or violate its assumptions?

2. (30 points) The New York Times of October 5, 1993 reported the following information in the Credit Markets section:

The yield on the 10-year (coupon-bearing, with coupons paid every six months) note fell to 5.32 percent from 5.33 percent. The yields on short-term Treasury notes were a little lower as some investors may have bought them because they were a less risky investment than long-term maturities. The price of the two-year note was up 1/32 as the yield fell to 3.81 percent from 3.83 percent.

But at the weekly auction of Treasury bills, the discount rates were up sharply. The average discount rate on three-month bills was 2.96 percent, up from 2.90 percent last week, and the average discount rate on six-month bills was 3.08 percent, up from 3.02 percent.

• a. Assuming that all these securities were issued Oct. 4, 1993, compute the forward rate that applies to the period Jan. 4, 1994 to April 4, 1994. (7 points)
• b. If liquidity premiums are constant, what can you infer about the change in the expected short rate for the period Jan. 4, 1994 to April 4, 1994? (8 points)
• c. Assuming that there is no change in real rates, what information do the bond price changes provide regarding the prognosis for inflation? (8 points)
• d. What do these rate changes imply for the duration of the three month bill, the six-month bill, and the ten year note? (7 points)

3. (20 points) Consider the Treynor-Black model. The alpha of an active portfolio is 2%. The expected return on the market index is 16%. The variance of return on the market portfoli is 4%. The nonsystematic variance of the active portfolio is 1%. The risk-free rate of return is 8%. the beta of the active portfolio is 1. What is the optimal proportion to invest in the active portfolio?

4. (25 points) Two investment advisors are comparing performance. The following information is available.

1. Advisor A's portfolio averaged a 19 percent rate of return; advisor B's averaged a 14 percent rate of return.
2. The beta of A's portfolio was 1.5.
3. The variance of B's portfolio return was less than that of the market portfolio.
4. The following multi index model works well in the sense of producing covariance estimates similar to that produced by a fullblown portfolio theory (Markowitz) model:

   R_i = a_i + b_i R_M + c_i R_I + e_i , where

   • R_i = return on stock i
   • R_M = return on the true market portfolio
   • R_I = the rate of inflation
   • e_i = stock specific shock
5. Investors are mean-variance optimizers.
6. There are no trading frictions in the market.
7. All assets are tradeable.
8. Cov(R_M, R_I) = 0.

a. Can you tell which advisor was a better predictor of individual stocks (aside from the issue of general movements in the market)?

b. If the T-bill rate were 6 percent and the market return during the period were 14 percent, which advisor would be the superior stock selector?

c. What if the T-bill rate were 3 percent and the market return were 15 percent?

Solutions:

3. 100%

4 i. We see from the fact that B's portfolio variance is less than that of the market that his portfolio's beta must be less than unity.

ii. From the information given, we see that the CAPM applies.

a. To see which advisor was a better predictor, we look at their alphas. Without information on the paramters of the SML, we cannot say which one is better.

b. If r_f = 0.06 and r_M = 0.14, then:

₁ = .19 -[0.06+1.5(.14-.06)] = .19-.18=.01

₂ > .14 -[0.06+1.0(.14-.06)] = .16-.14=.00

The first advisor seems to have a better ability to pick undervalued stocks, if the second advisor's beta is unity. If it is small enough, then the second advisor would turn out to be better; we can, therefore, not say for sure who is better.

c. If r_f = 0.03 and r_M = 0.15, then

₁ = .19 -[0.03+1.5(.15-.03)] = .19-.21=-0.02

₂ > .14 -[0.03+1.0(.15-.03)] = .16-.15=-.01

In this case, the first advisor seems to be buying overvalued stocks; hence his selection ability is worse than worthless. With the largest possible beta of 1, the second advisor is also doing badly, but still not as bad as the first advisor.

• ..Make all your assumptions explicit.
• ..Show all steps and please write legibly.
• ..Show all formulae clearly.

1. (30 points) Suppose you have the following information:

Security	Portfolio weight	Beta	Expected Return	i
A	.25	.50	.40	.07
B	.25	.50	.25	.05
C	.50	1.00	.21	.07

= .06

a. What is the beta factor of the three stock portfolio?

b. What is the expected return on the portfolio?

c. Given the assumption of the single-index model, what is the residual variance of each of the above stocks?

d. Under the assumption of the single-index model, what is the variance of the portfolio?

e. Given the actual covariances between the stocks' returns, _A,B = .02, _A,C = .035,

_B,C = .035, what is the portfolio variance?

f. Why might the actual covariances differ from those obtained under the assumption of the single-index model?

2. (15 points) Suppose you have $10,000 to invest and would like to sell $5,000 in stock B short to invest in stock A. Assume that the covariance between the returns on stocks A and B is zero. Calculate the expected rate of return and standard deviation.

Stock	A	B
E(r)	.12	.02
(r)	.08	.10

3. (10 points) If market volatility increases by 50%, what would you expect will happen to expected returns, assuming that the average degree of risk-aversion remains constant? Answer concisely.

4. (15 points) On May 1, Ivy Olson sold short 100 shares of Topeka Associates stock at $25 per share and bought on margin 200 shares of Columbus Company stock for $40 per share. The inital margin requirement was 50%. On June 30, Topeka stock sold for $36 per share and Columbus stock sold for $45 per share. Determine whether Ivy's account is restricted as of June 30; i.e. can she withdraw cash from her account.

5.(30 points) An investor is faced with the problem of finding the efficient portfolio with an expected return of 8% when the market consists of two risky assets with the following characteristics:

Covariance between r₁ and r₂ = .0003

The return available on the riskless asset is r = 5%. Find the corresponding efficient portfolio consisting of the riskless and the risky assets. Does the investor borrow or lend at the risky rate?

Go to P.V. Viswanath's Home Page