|
Midterm
- The midterm is closed book. However, you are allowed to bring in one 8.5"x11" sheet, containing anything you wish.
- Time allowed is 2 hours.
- Explain all your steps; correct answers without explanations may not be given any credit at all.
- Show all your computations and formulae. Make all your assumptions explicit. If your approach is correct, you will get some credit, even if your arithmetic answer is wrong. So concentrate on getting your logic right.
- If you answer a question, I have the discretion to award you some points, even if you are completely wrong. If you don't attempt the question at all, I can give you no points! So attempt every question.
- Questions 2 through 7 have to be done in-class. Question 1 is a take-home question. It is due by email by 11:59pm on Tuesday night, October 25.
1. (20 points) Read the following article from the online magazine ETF Profits (http://etf-profits.thestreet.com/articles/10/07/2011/buying-single-stocks-foolhardy), written by Matt Hougan and posted on October 7, 2011, and answer the following questions. Keep in mind that this article is from a website that promotes ETFs. Its arguments are not, for that reason, necessarily wrong; however, you need to be critical. The article by Jonathan Heller that it refers to can be found on another commercial website called the New Real Money (http://realmoney.thestreet.com/articles/10/07/2011/screening-large-dividend-plays). You may not be able to see the entire article, but you don't need to for the purpose of answering the question. Use all that you have learnt from the chapters that we have covered upto now, including Chapter 6 and 7.
- Explain the author's critique of Heller's dividend-based picks and his recommendations for using ETFs. What is your viewpoint? Support it.
- Can you think of counter-arguments as to why ETFs would not be the way to go? What would you substitute as an investment strategy instead of ETFs? Keep to the theme of this article, where he agrees essentially with Heller's basic point of using dividend-paying stocks in one's portfolio.
I spend a lot of time reading RealMoney. It provides a unique and valuable service to investors: near-real-time, intelligent reaction to breaking news in the financial markets.
If it has a flaw, it’s an obsession with single stocks.
It struck me when I was reading Jonathan Heller’s article on “Screening the Large Dividend Plays.” In one sense, it’s a perfectly reasonable piece. Noting that dividend-paying companies can smooth the ride for investors during times of crisis, Heller develops a screen to find large-cap dividend companies with strong financials.
His criteria are reasonable. It produces a list of 32 names ranging from ExxonMobil (XOM) to Lowe’s (LOW) to AFLAC (AFL), with an average yield of 2.8%.
Heller doesn’t talk about how to choose between the various stocks. He only suggests that this will be a group worth monitoring.
I couldn’t agree more. In fact, I’d go a step further and say that taking this research and buying any one of these stocks would be foolhardy, for three reasons.
First, it defeats the purpose of the exercise. The premise of Heller’s argument is that high-yielding stocks should help you ride out market volatility. That’s a great argument for buying all the stocks Heller outlines, but a terrible reason to pick one or two. One or two would concentrate your risk and would (by any reasonable definition) be riskier than owning the market as a whole.
Second, there’s no reason to think you would do it well. This is the big one. I’m sure that the readers of RealMoney are smarter than most people. I know they have more informational resources at their fingertips than most of their peers. But to select a firm like XOM or AFL out of the haystack and assume you’ll have an informational advantage over the rest of Wall Street? Well, that’s just crazy.
There are lots of very-well-paid analysts who spend their lives covering these firms and you’re unlikely to uncover a hidden gem or a mispriced large-cap. You may be right that the trend of dividend-payers-as-a-whole outperforming is real, but finding an undiscovered U.S. large-cap? Good luck.
Third, you don’t have to. This is important. There are 27 ETFs designed specifically to provide exposure to high-yielding stocks. That includes 12 focused in the U.S. market, drawn from eight different providers, tracking 12 distinct indexes. Each of those indexes uses some version of the criteria that Jonathan lays out.
The granddaddy of dividend funds, for instance, the iShares Dow Jones Select Dividend ETF (DVY), selects the highest-yielding stocks screened for dividend-per-share growth, dividend payout percentage, and liquidity. It currently yields 3.91%, higher than the 2.8% average yield screened by Heller’s criteria. The best-performing high-yield U.S. equity ETF over the past year is the First Trust Morningstar Dividend Leaders Fund (NYSEArca: FDL), which selects the highest yielding stocks after screening them for the ability to sustain those dividends long-term.
It’s currently yielding 4.24%, and has outperformed the S&P 500 by more than 5% over the past year.
There are other good choices as well.
I know why single stocks are attractive. It’s nice to think you have better information that your peers. It feels like you can get to know a company and how it’s stock trends. It’s fun to hit home runs.
But, in essence, you’re just playing hunches and unless you have the ability to massively diversify you’re taking on untoward risk. In a scenario like this, where you’re looking to smooth out your returns, single stocks are a mistake. The concept -- high-yielding stocks -- is a good idea. But an ETF is the way to play it.
2.(15 points) Old Economy Traders opened an account to short sell 3,000 shares of Internet Dreams at $81 per share. The initial margin requirement was 50%. (The margin account pays no interest.) A year later, the price of Internet Dreams has risen from $81 to $90, and the stock has paid a dividend of $3.00 per share.
- What is the remaining margin in the account?
- If the maintenance margin requirement is 30%, will Old Economy receive a margin call?
- What is the rate of return on the investment?
3. (10 points) Assume that you manage a risky portfolio with an expected rate of return of 17% and a standard deviation of 37%. The T-bill rate is 5%. Your client's degree of risk aversion is A = 2.1
- What proportion, y, of the total investment should be invested in your fund?
- What is the expected value and standard deviation of the rate of return on your client's optimized portfolio?
4. (10 points) Suppose that you have $1 million and the following two opportunities from which to construct a portfolio:
- Risk-free asset earning 7% per year.
- Risky asset with expected return of 27% per year and standard deviation of 40%.
If you construct a portfolio with a standard deviation of 28%, what is its expected rate of return?
5. (15 points) A pension fund manager is considering three mutual funds. The first is a stock fund, the second is a long-term government and corporate bond fund, and the third is a T-bill money market fund that yields a rate of 5%. The probability distribution of the risky funds is as follows:
| |
Expected Return |
Standard Deviation |
| Stock Fund (S) |
17% |
13% |
| Bond Fund (B) |
11 |
22 |
The correlation between the fund returns is 0.10. You require that your portfolio yield an expected return of 14%, and that it be efficient, on the best feasible CAL.
- What is the standard deviation of your portfolio?
- What is the proportion invested in the T-bill fund and each of the two risky funds?
6. (20 points) Answer any four of the following questions:
- Security A has expected return of 11% and standard deviation of 22%. Security B has expected return of 16% and standard deviation of 29%. If the two securities have a correlation coefficient of 0.6, what is their covariance?
- Suppose you have the following four investment possibilities:
| Investment |
Expected Return E(r) |
Standard Deviation |
| A |
0.12 |
0.29 |
| B |
0.15 |
0.35 |
| C |
0.24 |
0.38 |
| D |
0.29 |
0.44 |
Suppose further that your utility function is U = E(r) – (0.5) (A) (σ2), where A = 3.0. Which of the four investments above would you select, if you could only pick one of them?
- You purchased shares of a mutual fund at a NAV of $18.00 per share at the beginning of the year and paid a front-end load of 5.75%. If the securities in which the fund invested increased in value by 12% during the year, and the fund’s expense ratio was 0.75%, what would your return be if you sold the fund at the end of the year?
- You purchased Research in Motion (RIMM) for $79.83 per share. Its current price is $71.17. If the price goes below $70.00 per share you think it could be headed even lower. What kind of order would you call in to your broker to avoid bigger losses?
- A 6.25% 25-year municipal bond is currently priced to yield 8.7%. What is the equivalent taxable yield that this bond would offer for a taxpayer in the 25% marginal tax bracket?
7. (15 points) Answer any three of the following questions:
- Who are specialists? What is their role?
- How is the DJIA constructed?
- The Sharpe Ratio implicitly assumes normality because it uses standard deviation as a measure of uncertainty. What measure of return-to-risk can we use if return distributions are not normal?
- What are TIPs?
Solutions to Midterm
1. a. Although the article refers to selecting stocks by dividend yield (described, presumably, in more detail in the other referenced article by Jonathan Heller), it doesn't discuss dividend yield, per se, too much. Rather, it points out the advantages of diversification and how this can be achieved with ETFs. The author, Matt Hougan, notes that Heller doesn't explain how to choose between the different dividend-paying stocks but rather focuses on the group. Hougan agrees that the stocks should be treated as a group, not as individual picks. (It seems that Hougan is inferring Heller's point of view by using an argument from silence. If Heller did indeed suggest holding one or a small group of his stock picks, Hougan would have to disagree with Heller, since his main issue is to push the benefits of ETFs.)
It also points out that markets are fairly efficient, although Hougan is willing to concede the point that strategies such as those suggested by Jonathan Heller might earn abnormal returns (Hougan notes that the FDL ETF has outperformed the S&P by more than 5% this year -- though, of course, there's no discussion of whether this adjusts for other risks and whether the difference is statistically significant).
This seems to be a bit of a contradiction and seems to be the result of the author's desire to promote specialized ETF strategies such as high dividend-yield ETFs, but at the same time downplay individual stock picking. Based on the information provided by Matt Hougan, himself, one gets the feeling that the existing dividend-based ETFs do not quite conform to the strategy that Jonathan Heller recommends. While one can cavil at the selective approach to market efficiency, the focus on diversification (within-strategy in the article) cannot be faulted.
b. Obviously, mutual funds (MF) are an alternative to ETFs. One would have to know whether Heller's suggested strategy is a short-term or a long-term strategy to figure out whether ETFs or MFs would be better. If it's not a strategy that requires keeping track of intra-day price movements, the ability to sell ETFs throughout the day may not be relevant. The relative trading costs of ETFs versus MFs also need to be taken into account, of course. MFs combine all trades for a given day into one trade and hence might have scale efficiencies. Asset management fees, in practice, seem to be lower for ETFs than for passively managed MFs.
2.a. The initial margin was: 0.50 × 3,000 × $81 = $121,500.
As a result of the increase in the stock price Old Economy Traders loses: $9 × 3,000 = $27,000.
Therefore, margin decreases by $27,000. Moreover, Old Economy Traders must pay the dividend of $3.00 per share to the lender of the shares, so that the margin in the account decreases by an additional $9,000. Therefore, the remaining margin is: $121,500 – $27,000 – $9,000 = $85,500. As a percentage of the loan (90x3000 = 270000), the margin is 85500/270000 = 31.67%
b. The percentage margin is: $85,500 / $270,000 = 31.67%, which is more than the required maintenance margin of 30%. So, there will be no margin call.
c. The equity in the account decreased from $121,500 to $85,500 in one year, for a rate of return of: (– $36,000 / $121,500) = -0.2963 = -29.63%
3. a. y* = [E(rP)-rf]/Aσ2P = (0.17-0.05)/(2.1x0.372) = 0.12/0.2875 = 0.4174. Therefore,
the client’s optimal proportions are: 41.74% invested in the risky portfolio and 58.26% invested in T-bills.
b. E(rC) = 5(1-y*) + 17y* = 5(0.5826) + 17(0.4174) = 10.00%; σC = 0.4174 × 37 = 15.44%.
4. You need a portfolio with a standard deviation of 28%. Since the portfolio standard deviation equals yσP, where y is the proportion in the risky asset and σP is the standard deviation of the risky asset, we have yσP = 28 or y = 28/40 = 0.7. Hence the expected return of the portfolio is 7(1-0.7) + 27(0.7) = 21%.
5. a. We first use the formula to find the tangent portfolio (in the formula below, treat D as the stock portfolio and E as the bond portfolio): 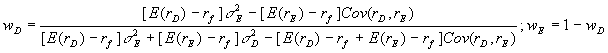
Solving, we find that the proportion in the stock fund is {(0.17-0.05)(0.22)2-(0.11-0.05)(0.13)(0.22)(0.1)}/{(0.17-0.05)(0.22)2+(0.11-0.05)0.132+(0.17-0.05+0.11-0.05)(0.13)(0.22)(0.1)} = (0.005808-0.0001716)/(0.005808+0.001014-0.0005148) = 0.893645; the proportion in the bond fund, therefore, is 1-0.893645 or 0.106355.
Using these numbers, we see that the expected return of the tangent portfolio is (0.893645)(17) + (0.106355)(11) = 16.36%; the variance of the portfolio is 0.89362 (132) + (0.10642)(222) + 2(0.1)(0.8936)(0.1064)(13)(22) = 207.9382. The standard deviation, therefore, is the square root or 14.42%.
If we require that our portfolio yield an expected return of 14%, then we can find the corresponding standard deviation from the optimal CAL. The equation for this CAL is: E(rC) = rf +{[E(rP)-rf]/σP}σC; i.e. 0.14 = 0.05 + [(0.1636-0.05)/0.1442)]σC. Solving, we find σC = 11.42%.
b. To find the proportion invested in the T-bill fund, remember that the mean of the complete portfolio (i.e., 14%) is an average of the T-bill rate and the optimal combination of stocks and bonds (P). Let y be the proportion invested in the portfolio P. The mean of any portfolio along the optimal CAL is E(rC) = (1 – y) × rf + y × E(rP) = rf + y × [E(rP) – rf] = .05 + y × (.1636 – .05); setting E(rC) = 14% we find: y = .79225 and (1 − y) = .2077 (the proportion invested in the T-bill fund).
To find the proportions invested in each of the funds, multiply 0.79225 times the respective proportions of stocks and bonds in the optimal risky portfolio:
Proportion of stocks in complete portfolio = 0.79225 × 0.8936 = 0.7080; the proportion of bonds in complete portfolio = 0.79225 × 0.1064 = 0.08426.
6.
- The covariance is the product of the covariance and the standard deviations; hence it works out to (0.6)(0.29)(0.22) = 0.03828.
- The utility scores of the four options are presented below. Investment C would provide the highest utility to the investor described.
U(A) = .12 - (.5) (3) (.292) = -0.00615
U(B) = .15 - (.5) (3) (.352) = -0.03375
U(C) = .24 - (.5) (3) (.382) = 0.02340
U(D) = .29 - (.5) (3) (.442) = -0.00040
Note that the sign of the resulting calculations is not meaningful. Only the ranking is important, with the highest utility being the most favorable.
- We will first assume that the order was for one share. Since you paid a front-end load of 5.75%, your actual cost was 1.0575(18) = 19.035. The end-of-year price of the share was 18(1.12) or 20.16. However, since the fund's expenses have to be paid, as well, the value in the fund at the end of the year would only be 20.16(1-0.0075) = 20.0088. Hence the actual return, net of expenses would be 20.0088/19.035 -1 = 5.116%.
Let's now assume that you invested $18 in all. In that case, since the fund has a front load, only (1-.0575) times NAV is actually invested and growing. Therefore the initial investment equals $18 * .9425 = $16.965. The money invested will grow at 12% minus the 0.75% fees (or 11.25%). The ending balance in your account will equal $16.97 * (1.1125) = $18.8736. Your initial out of pocket investment was $18.00, so your return is ($18.8736-18.00)/$18.00 = 4.85%.
- You would place a stop-loss order with a stop at $70. If the price dipped below $70, then the broker would be authorized to sell it immediately at the market price.
- The equivalent taxable yield is the yield divided by the quantity one minus the tax rate or rm/(1-t). Therefore, the equivalent taxable yield is (0.087 / 0.75) = 11.6%.
7.
- A specialists is an employee of an NYSE member firm, who has the responsbility of making continuous markets, matching buyers with sellers, keeping investors informed, committing capital when needed, standing accountable for the market in his or her stocks and ensuring that all customer orders have an equal opportunity to interact and receive the best possible execution (according to the NYSE). In other words, the specialist is supposed to maintain a fair and orderly market, which means that there should not be big jumps in the price. The specialist is supposed to commit his own capital to trading and ensuring that this does not happen.
- The DJIA is constructed as a simple average of the prices of the 30 stocks that make up the index; however, this average is then multiplied by a factor that varies from time to time when there is a change in the index composition or when there is a stock split or a stock dividend for one of the stocks in the index.
- If return distributions are not normal, then we can use the Sortino ratio, which is defined as the excess return over the risk-free rate divided by the LPSD or the lower partial standard deviation.
- TIPs are Treasury Inflation-Protected Securities. The principal of a TIPS increases with inflation and decreases with deflation, as measured by the Consumer Price Index. When a TIPS matures, you are paid the adjusted principal or original principal, whichever is greater. TIPS pay interest twice a year, at a fixed rate. The rate is applied to the adjusted principal; so, like the principal, interest payments rise with inflation and fall with deflation.
Final
Notes:
- If your answers are not legible or are otherwise difficult to follow, I reserve the right not to give you any points.
- If you cheat in any way, I reserve the right to give you no points for the exam, and to give you a failing grade for the course.
- You may bring in sheets with formulas, but no worked-out examples, or definitions, or anything else.
- You must explain all your answers. Answers without explanations may not receive any points.
- For quantitative questions, you must write down the formula; then show what the numerical equivalents for the variables in the formula are, and then provide the numerical answer. You may use a calculator to obtain the answer, but you still have to follow the requirements stated here.
- All questions must be answered on the sheets provided only.
- Question 1 from Part A is compulsory; answer any two other questions from Part A; three questions from part B and three questions from part C.
- You may substitute the media article question for any other question.
Part A |
Question Attempted |
Maximum Points |
Points Obtained |
First |
1. |
12 |
|
Second |
|
11 |
|
Third |
|
11 |
|
|
|
|
|
Part B |
|
|
|
First |
|
11 |
|
Second |
|
11 |
|
Third |
|
11 |
|
|
|
|
|
Part C |
|
|
|
First |
|
11 |
|
Second |
|
11 |
|
Third |
|
11 |
|
Total |
|
|
|
Part A:
1.
Assume you have a 1-year investment horizon and are trying to choose among two bonds. Both have the same degree of default risk and mature in 10 years. The first is a zero-coupon bond that pays $1,000 at maturity. The second has a 6.6% coupon rate and pays the $66 coupon once per year. Assume that the coupon bond was originally issued at par. |
|
a. |
If both bonds are now priced to yield 6% to maturity, what are their prices? |
b. |
If you expect their yields to maturity to be 5% at the beginning of next year, what will their prices be then? What is your before-tax holding-period return on each bond? If your tax bracket is 30% on ordinary income and 20% on capital gains income, what will your after-tax rate of return be on each? |
|
|
2.
You observe the following term structure: |
|
Effective Annual YTM |
1-year zero-coupon bond |
8.0% |
2-year zero-coupon bond |
8.1 |
3-year zero-coupon bond |
8.2 |
4-year zero-coupon bond |
8.3 |
|
If you believe that the term structure next year will be the same as today's, what will the expected 1-year return be on the 1-year zero and on the 4-year zero? |
3.
Consider the following multifactor (APT) model of security returns for a particular stock. |
Factor |
Factor Beta |
Factor Risk Premium |
Inflation |
1.8 |
7.0% |
Industrial production |
1.2 |
10.0 |
Oil prices |
.8 |
5.0 |
|
a. |
If T-bills currently offer a 3% yield, find the expected rate of return on this stock if the market views the stock as fairly priced. |
b. |
Suppose that the market expected the values for the three macro factors given in column 1 below, but that the actual values turn out as given in column 2. Calculate the revised expectations for the rate of return on the stock once the "surprises" become known. |
Factor |
Expected Rate of Change |
Actual Rate of Change |
Inflation |
8% |
7% |
Industrial production |
6 |
10 |
Oil prices |
3 |
0 |
|
4.
Consider a bond (with par value = $1,000) paying a coupon rate of 6% per year semiannually when the market interest rate is only 3% per half-year. The bond has 3 years until maturity. |
a. |
Find the bond's price today and 6 months from now after the next coupon is paid. |
b. |
What is the total (6-month) rate of return on the bond? |
Part B:
- Why did Roll claim that the CAPM is not testable?
- You are socializing with your colleagues when the subject of investing arises. Ed tells the group about his amazing success, saying that he has realized an 18% return in the last two months. The market was down 3% during that period. Other group members start to ask for his advice on what securities to buy and he names several possibilities. What behavioral qualities is Ed demonstrating and why might they cause problems for people who follow his advice?
- Assume that you are using a two-factor APT model to find the expected return on a stock. The factors, their betas, and their assumed risk premiums are shown in the table below. The risk-free rate is 4.8%.
Factor |
Factor Beta |
Assumed Factor Risk Premium |
A |
1.7 |
2.0% |
B |
0.9 |
10.5% |
- What is the expected return on the stock if it is fairly priced?
- Now suppose that the factor risk premiums you used are found to be incorrect. The true factor risk premiums are shown below. Recalculate the expected return on the stock based on the true factor risk premiums.
Factor |
Factor Beta |
True Factor Risk Premium |
A |
1.7 |
3.5% |
B |
0.9 |
9.0% |
- A coupon bond is reported as having an ask price of 108 (that is, 108% of the $1,000 par value) in the Wall Street Journal. If the last interest payment was made two months ago and the coupon rate is 12%, the invoice price of the bond will be ________.
Part C:
- What are some common covenants in bond indentures?
- What is regret avoidance and how does it affect stock price movements?
- It costs time and money to collect information. If all information is incorporated in stock prices, then there would be no incentive to collect this information. On the other hand, if no information is collected by market participants, then this information cannot be incorporated into market prices. How would you explain this seeming paradox?
- If the CAPM holds, the APT must hold and vice-versa. True or false? Explain.
- How can you synthesize a forward contract using spot securities?
Media Article
Read the article below and answer the following questions (the first two sections should be enough to answer the questions):
- What is the connection between long-term yields, short-term yields and market expectations?
- Use your answer in part (a) to explain why should a steep yield curve imply a rapid economic upswing?
- Why do the authors disagree?
Yield curve predicting inflation, not growth surge
Reuters, Thu, Dec 24 2009, By Chris Reese and Emily Flitter - Analysis
NEW YORK (Reuters) - A record wide gap between the yields of two-year and 10-year U.S. Treasury notes may have more to say about the threat of inflation down the road than the popular view that it's a harbinger of dramatic recovery.
Market wisdom dictates that when the yield curve is steep, a rapid economic upswing is in store. Earlier this week, the spread between yields on two-year and 10-year notes reached a record-wide 287 basis points.
But many analysts believe the steep curve may mean something different this time -- though they've been wrong on such assumptions before.
This time, some say the steep curve presages a potential jump in inflation, as the Federal Reserve prints massive amounts of money to prop up the economy. Others point to the increasing supply of longer-dated Treasuries, as the government extends the life of its debt while investors, worried about a rate increase, crowd into shorter-dated notes and bills.
"If you look at the back end of the curve it's predicting higher rates somewhere out at year four -- inflation would be a threat that far out. That is what the yield curve is predicting here, that this policy is opening the door to future inflation," said Ronti Pal, head of U.S. dollar rates trading at Barclays Capital in New York.
INFLATION AHEAD
The Treasury is expected to issue as much as $2 trillion in government debt in 2010. The size of the planned issuance has stoked fears that the new money flooding the economy will depress the dollar and drive prices sharply higher.
Inflation erodes the value of Treasury debt over time. The recent dip in longer-dated Treasury prices and the spike in the yield curve reflects investors' worries that real returns on their longer-dated U.S. bonds could fall.
The yield curve has in the past not been a strong predictor of inflation, but in those instances rates were notably higher than now and acted as more of a constraint on prices. The two-year note is currently yielding 0.92 percent. At the end of November, it hit a closing low of 0.66 percent, lower than at any time in the last 25 years.
"The vast majority of people think that the next phase of the interest rate cycle is going to be one where the market and the (Federal Reserve) more broadly is worried about inflation -- that means that the overall risk is that we're going to have high inflation that leads to a steeper curve," said Ian Lyngen, senior government bond strategist at CRT Capital Group in Stamford.
Since the Fed has emphasized that it will keep interest rates low for an "extended period of time," investors generally feel comfortable buying shorter-dated notes. But the more distant future of interest rates isn't clear. And the supply of longer-dated notes and bonds is set to grow faster than the supply of shorter-term securities.
Just as the current steepness of the yield curve suggests that the market expects inflation, the development of a weaker recovery with slower growth could cause the curve to flatten a bit.
"It is safe to say we will probably have growth that may warrant a positive yield curve, but maybe it doesn't need to be as steep as it is because ... of the headwinds that the economy is facing," said David Coard, head of fixed-income sales and trading at The Williams Capital Group in New York.
If economic indicators next year offer less robust readings, investors may return more eagerly to longer-dated Treasuries.
UNHEEDED WARNING
To be sure, investors may want to think twice before shrugging off the predictive powers of the yield curve. The curve "inverted" through much of 2006 and early 2007, with the yield on 10-year notes falling below two-year note yields. An inverted yield curve has often preceded recessions over the past 70 years, including the Great Depression.
The majority of economic analysts shrugged off the curve inversion, however, claiming the situation was atypical because a voracious appetite for long-dated bonds from overseas, especially China, was keeping long-dated yields unusually low.
However, the U.S. economy descended into one of the worst recessions in its history at the end of 2007 following the collapse of the U.S. subprime mortgage market and then the financial crisis.
"In hindsight, people should have paid more attention to it in 2006 and 2007," said John Canally, investment strategist and economist with LPL Financial in Boston.
Still, Cannally suggests the yield curve's predictive ability is in question, though he says it should portend at least a steady improvement in demand. "It tells you the current expansion is sustainable through 2010," he said, adding "it may be less predictive, but not 'un-predictive' -- it bears watching closely."
(Additional reporting by Richard Leong and Emily Flitter; Editing by Lesli
Solutions to Final
1.
a. |
Zero coupon |
6.6% coupon |
Current prices |
$558.39 |
$1,044.16 |
|
|
|
| b. Price 1 year from now |
$644.61 |
$1,113.73 |
Price increase |
$ 86.22 |
$ 69.57 |
Coupon income |
$ 0.00 |
$ 66.00 |
Pre-tax income |
$ 86.22 |
$135.57 |
Pre-tax rate of return |
15.44% |
12.98% |
Taxes** |
$ 20.60 |
$ 33.38 |
After-tax income |
$ 65.62 |
$102.19 |
After-tax rate of return |
11.75% |
9.79% |
* In computing taxes, we assume that the 7.6% coupon bond was issued at par and that the decrease in price when the bond is sold at year end is treated as a capital loss and therefore is not treated as an offset to ordinary income. |
** In computing taxes for the zero coupon bond, $33.51 is taxed as ordinary income; the remainder of the price increase is taxed as a capital gain. |
2.
|
|