|
Midterm
- The midterm is closed book. However, you are allowed to bring in one 8.5"x11" sheet, containing only formulas.
- Time allowed is 2 hours.
- Explain all your steps; correct answers without explanations may not be given any credit at all.
- Show all your computations and formulae. Make all your assumptions explicit. If your approach is correct, you will get some credit, even if your arithmetic answer is wrong. So concentrate on getting your logic right.
- If you answer a question, I have the discretion to award you some points, even if you are completely wrong. If you don't attempt the question at all, I can give you no points! So attempt every question.
- You can invest in two different risky portfolios:
|
|
Expected Return
|
Standard Dev of Returns
|
| Evergreen
|
9%
|
12%
|
| Fallcolor
|
16%
|
20%
|
The correlation of returns between the two portfolios is 0.4. Assume A = 4.
- (10 points) If you had $10000 to invest, how much would you invest in each portfolio, if you could also borrow and lend at 4% p.a.?
- (5 points) How much would you invest in the risk-free asset?
- Dupont stock (DD) closed on October 15, 2012 at $49.01. Suppose you had bought 500 shares at the close and financed it partly by using your margin privileges with your broker, who allows you to buy at 50% initial margin.
- (10 points) If his maintenance margin is 30%, how much would the price have to change before you would have to put up margin?
- (10 points)Suppose you had sold short instead of buying on margin. Assume, again, that initial margin on short sales is 50%. If the maintenance margin on short sales is 30%, at what price would you have to put up fresh margin?
- (5 points)Suppose brokers decided on their own policies regarding maintenance margins. If you discovered that your broker’s maintenance margins were higher for stock A than for stock B, what information would you glean (obtain) from that about the two stocks?
- Probabilities for three states of the economy and probabilities for the returns on a particular stock in each state are shown in the table below:
| State of the Economy |
Probability of economic state |
Stock Performance |
Probability of Stock Performance in Given Economic State |
| Good |
0.3 |
Good |
.6 |
| |
|
Poor |
.4 |
| Neutral |
0.4 |
Good |
.5 |
| |
|
Poor |
.5 |
| Poor |
0.3 |
Good |
.2 |
| |
|
Poor |
.8 |
- (5 points)What is the probability that the economy will be neutral and the stock will experience poor performance?
- (5 points)Is the stock performance independent of the state of the economy?
- (5 points)What is the expected return on the stock, assuming that the state of the economy is good?
- (5 points)If a good stock return is 15% and a bad stock return is 5%, what is the expected return on the stock?
- Answer any five of the following questions (25 points):
- How is the DJIA constructed?
- What is the role of specialists?
- What is the problem with fragmentation?
- Define the Sharpe ratio? What is its function?
- What are the advantages of ETFs?
- If the Fisher Hypothesis is correct, what should be the correlation between inflation rates and nominal real rates? Explain.
- What is the separation property? What is the importance of the separation property?
- Read the article below from the NY Times of August 17, 2008 (http://www.nytimes.com/2008/08/17/business/economy/17stra.html?_r=0) by Mark Hulbert and answer the following questions:
- (10 points) The author claims that investors have wrongly believed that higher inflation is bad for stocks and thus have undervalued stocks. Explain what the misconception of investors is that, according to the author, has led to this undervaluation.
- (10 points) According to the author, what is the correlation between nominal returns on equities and inflation? Explain with reference to the specific statement of the author.
Illusions About Inflation
THERE is widespread concern that high inflation — running at a 5.6 percent annual rate in the 12 months through July — could hurt the stock market. But this investor worry may be yet another example of money illusion: the confusion of nominal prices with their inflation-adjusted equivalent.
The notion that inflation is bad for stocks appears to make a good deal of sense. What’s more, there is reason to believe that this perception — mistaken though it may be — has sometimes driven down stock prices.
With inflation at 6 percent, for example, a dollar of profit that a company will earn a year from now is worth only 94 cents in today’s dollars. But if inflation were just 1 percent, as it was in early 2002, that dollar earned a year from now would be worth 99 cents today. Such differences add up, especially as investors consider a company’s earning power over many years.
Put a different way, if other things are equal, the value of a company’s future earnings will be lower to the extent that inflation is higher. That would make the company’s stock less valuable, and if investors went no further in their analysis, stock prices would deserve to decline.
But other things are not equal when it comes to stocks and inflation. Over the last eight decades, corporate profits have tended to grow faster when inflation is higher. In such periods, companies have been able to pass along higher costs to their customers. As a result, even though higher inflation leads to a greater discounting of future years’ earnings, those earnings tend to be bigger than they would have been otherwise. The net result is that the current value of a company’s future earnings remains relatively stable in the face of rising inflation.
This was the strong conclusion of a study conducted five years ago by John Campbell and Tuomo Vuolteenaho, both economics professors at Harvard at the time. (Mr. Campbell is still at Harvard; Mr. Vuolteenaho is not. Both are now partners at Arrowstreet Capital, a money management firm based in Boston.) Their study, “Inflation Illusion and Stock Prices,” was in the May 2004 issue of the American Economic Review.
In an interview, Professor Campbell emphasized that their study does not mean investors are wrong to worry about developments like high oil prices, which may be damaging the economy in specific ways while also contributing to inflation. But, he said, “inflation should not be an additional source of concern above and beyond those other developments.”
Of course, investors suffering from money illusion could knock down stock prices further than they deserve to be. Historically, this has sometimes occurred as inflation has begun to heat up, as investors extrapolate too low a growth rate for corporate profits into the future.
ONE of the best-known illustrations occurred during the high-inflation 1970s. For the 10 years through 1979, the Standard & Poor’s 500-stock index had an annualized gain of just 1.6 percent, a far cry from the historical average of close to 10 percent. That dismal performance helped to lower the index’s price-to-earnings ratio to a low of 6.8 by the end of that decade, according to data from Robert J. Shiller, the Yale finance professor. The comparable ratio today is around 20.
Franco Modigliani, who in the late 1970s was a finance professor at the Massachusetts Institute of Technology, realized that money illusion was a major factor in the market’s dismal performance in that decade. In a 1979 article written with Richard A. Cohn, then also an M.I.T. professor, he argued that stocks, in fact, were a good long-term hedge against inflation and that the stock market was therefore significantly undervalued. The strong bull market of the 1980s and 1990s vindicated their argument, and in 1985 Professor Modigliani was the Nobel laureate in economics. (Both men are now deceased.)
There’s no way to know, of course, whether investors will make the same mistake in the next few years as they did in the 1970s, pushing stock prices down to unjustifiably low levels. But even if they did, it doesn’t necessarily mean stocks deserve to be cheaper when inflation is high.
As Clifford S. Asness, managing principal at AQR Capital Management, a hedge fund firm, put it in an e-mail message, “It is a strange leap to observe that investors consistently make an error, and then recommend that error to current investors based on precedent.”
In any case, if inflation keeps heating up and investors fall victim to money illusion, stocks may well decline for a while. But if history is any guide, such weakness would signal an excellent long-term buying opportunity.
Solutions to Midterm
1.
Suppose we consider Evergreen to be asset D, and Fallcolor to be asset E, we can use the formula below:
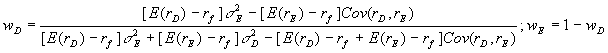
Plugging numbers into the formula, we get the tangent portfolio as:
wD = (9-4)(20)(20)-[(16-4)(12)(20)(0.4)] ÷ [(9-4)(20)(20)+(16-4)(12)(12)-(9-4+16-4)(12)(20)(0.4)] = 0.40458;
Hence wE = 1-0.40458 = 0.59542.
The expected return on this portfolio is (0.40458)(9)+(0.59542)(16) = 13.16794%
The variance is given by (0.40458*12)2+(0.59542*20)2+2(0.40458)(0.59542)(12)(20)(0.4) = 211.6324, so that the standard deviation is the square root or 14.54759%.
We can now use the formula y* = [E(Rport) – Rf]/(0.01AVar(Rtgtport)) to get y* = 9.16794/[(0.01)(4)(211.6324)] = 1.083; hence it would be necessary to borrow 8.3% of the investor’s total investment.
Hence you would borrow (0.083)(10000) = $830. This would be invested as follows: (0.40458)(10830) = $4381.60 in the Evergreen fund and $6448.40 in the Fallcolor fund.
2. a. Total purchase is 49.01x500 = $24,505. Initial margin is 50%, so the investor would have put up 50% of this amount, viz. $12252.50; the loan would also be $12252.50. Actual margin is computed as Equity/Total Value of Assets. Suppose the stock price is P, then actual margin would be (500P-12252.5)/500P. Setting this equal to 0.3 and solving for P, we get $35.01
b. In this case, the amount of the loan would be 500P; the total amount of assets would be (1.5)(24505), and the equity would be (1.5)( 24505) - 500P. The margin is computed as a fraction of the loan, viz. 500P, so we solve [(1.5)(24505) - 500P]/500P = 0.3. The solution is P = $56.55.
c. This would imply that stock A is more volatile than stock B.
3. a. This is the joint event that the economy is neutral and that the stock performance will be poor. This is the product (0.4)(0.5) = (0.2) or 20%.
b. The answer is no – since the conditional probabilities vary according to the state of the economy.
c. If the state of the economy is good, the expected return will be (0.6)(15) + (0.4)(5) = 11%.
d. We have to compute the expected return in the other two possibilities – these will be (0.5)(15) + (0.5)(5) = 10% and (0.2)(15) + (0.8)(5) = 7% for the neutral and poor states respectively. The associated probabilities of the three states of the economy are 0.3, 0.4 and 0.3; so weighting the three expected returns by these probabilities, we get (0.3)(11)+(0.4)(10)+(0.3)(7) = 9.4%
4.
a. The DJIA is simply the average price of the 30 stocks in the index, divided by the divisor that is valid at the given time.
b. Specialists are charged with maintaining a fair and orderly market. In particular, this means that if there is significant market movement in a particular direction, the specialist should be resisting the trend so as to make price changes smaller. In addition to this role, the specialist makes a market by offering to buy and sell the stock at all times, and acts as a catalyst by bringing buyers and sellers together.
c. The problem with fragmentation is that it reduces liquidity in each market. The number of traders in each market will be lower than if there were a centralized market; the bid-ask price in each market will be higher than if the market were centralized.
d. The Sharpe ratio is defined as [E(Rp)-Rf]/Std Dev(excess returns), where excess return= Rp-Rf. Its function is to operate as a reward-risk ratio for portfolios.
e. ETFs can be traded at any time of the day, like a stock. There are tax consequences to the investor only if s/he trades the ETF, unlike a share in a mutual fund, where the overall trading of the fund can result in capital gains realizations for the investor.
f. The correlation between inflation and nominal interest rates should be 1, since nominal rates should keep up with inflation. There should be no correlation between inflation and the real rate because under the Fisher hypothesis, the real sector is independent of the monetary sector.
g. The separation property says that the choice of the risky portfolio is independent of the risk preference of the investor – this portfolio is the same for all investors. However, the choice of how much to invest in this risky portfolio and how much to invest in the risk-free asset depends on the investor’s risk aversion. The reason that this is important is that there can be a single mutual fund, replicating the single risky portfolio, that all investors can invest in; this would reduce trading costs.
5.
a. The author says that investors have incorrectly believed that higher inflation is bad for stocks and thus have undervalued stocks. According to him, investors have taken future profits as being uncorrelated with inflation. Hence the higher inflation is, the higher interest rates would be, and equity profits would be discounted at higher rates; hence stock prices would be lower. In fact, when inflation is high, corporate profits rise, as well. As he notes, “Over the last eight decades, corporate profits have tended to grow faster when inflation is higher.”
b. The author seems to believe that, in the long run, investors’ money illusion would be dispelled. If this happens, then (as in the 1980s), equities would end up being a good hedge against inflation. In this case, the correlation between nominal returns on equities and inflation should be high, close to 1. This can be understood from two statements that the author makes: one, "In a 1979 article written with Richard A. Cohn, then also an M.I.T. professor, he argued that stocks, in fact, were a good long-term hedge against inflation and that the stock market was therefore significantly undervalued. The strong bull market of the 1980s and 1990s vindicated their argument" and two, " if history is any guide, such weakness would signal an excellent long-term buying opportunity."
Final
Notes:
- If your answers are not legible or are otherwise difficult to follow, I reserve the right not to give you any points.
- If you cheat in any way, I reserve the right to give you no points for the exam, and to give you a failing grade for the course.
- You may bring in one sheet with formulas, but no worked-out examples, or definitions, or anything else.
- You must explain all your answers. Answers without explanations may not receive any points.
- For quantitative questions, you must write down the formula; then show what the numerical equivalents for the variables in the formula are, and then provide the numerical answer. You may use a calculator to obtain the answer, but you still have to follow the requirements stated here.
1. Read the article below from the Nov. 8, 2012 edition of the Economist and answer the following questions:
Academic papers and stockmarket returns
Keep digging: The treasure buried in academic papers about market anomalies
Like miners panning for gold, number-crunchers love the stockmarket. There are thousands of different securities prices to analyse, decades-worth of data to dissect. Academics can make their reputation by discovering an anomaly in prices, such as smaller companies outperforming the index over the long term.
But are these anomalies a route to riches or the equivalent of iron pyrite (“fool’s gold”)? They may just be data quirks—what statisticians call “noise”. Another possibility is that investors read the academic papers and then go into the market to take advantage of the anomaly. If so, as they buy the “cheap” stocks and sell the “expensive” ones, the discrepancy should gradually disappear.
The answer may be found in, yes, another academic paper. The authors looked at 82 separate anomalies discovered by academics and examined the returns from the suggested strategy both before and after publication. They find that investors can still earn excess returns after publication, but that these returns fall by around a third.
The decline is probably caused by investor activity: trading volumes in shares related to the anomalies tend to increase after academics have revealed them. But why don’t the anomalies disappear altogether?
One reason may be constraints on investor behaviour. Some strategies require investors to go short (bet on falling prices) or use borrowed money: pension funds and mutual funds are unable to do so. Another reason may be that trading costs reduce the scope for profits. Anomalies disappear more quickly if the stocks involved are large and liquid, and thus less costly to trade.
Even if their discoveries cannot be traded on, finance professors will keep mining the data. As well as the academic kudos involved in finding an anomaly, their insights might just land them a job at a hedge fund. Trading a university salary for a share of a fund’s performance fee is a really attractive example of profitable arbitrage.
- (5 points) How do we know that investors actually pay attention to academic studies that investigate stock market pricing anomalies?
- (10 points) Why don't stock pricing anomalies disappear after they have been uncovered by academic researchers?
- (10 points) Why would pricing relationships implied by arbitrage pricing theories not hold exactly in practice, even if the underlying theory is true? Why would pricing relationships implied by risk-return dominance arguments not hold exactly in practice, even if the underlying theory is true?
2. (20 points) The following table shows yields to maturity of zero-coupon Treasury securities.
| Term to Maturity (Years) |
Yield to Maturity (%) |
1 |
3.5% |
2 |
4.5% |
3 |
5% |
4 |
5.5% |
5 |
6% |
10 |
6.6% |
- Calculate the forward 1-year interest rate for year 3.
- Assume that a few months earlier, the forward 1-year rate of interest for that year had been significantly higher than it is now. What factors could account for the decline in the forward rate?
- How would you explain the upward sloping yield curve shown in this table?
- Why would you expect any yield curve to become flat at higher maturities?
3. (12 points) According to Muhammad Yunus, social businesses would be allowed to return an investor's initial investment in the company. However, no payments would be made to an investor beyond that. In particular, no dividends would be paid. Under these circumstances, why would anybody wish to buy a share of such a social business firm? How would a share in such a firm be valued in a social stock market? The price of an ordinary dividend-paying stock varies according to the market's estimation of the present value of the stock's future dividends to shareholders. What would determine the day-to-day change in prices of the share of a social business?
4. (10 points) Answer any two of parts a. b. or c. below:
a. An investor believes that a bond may temporarily increase in credit risk. Which of the following would be the most liquid method of exploiting this? Explain.
- The purchase of a credit default swap.
- The sale of a credit default swap.
- The short sale of the bond.
b. What would be the likely effect on the yield to maturity of a bond resulting from an increase in the issuing firm's quick ratio? Explain.
c. A 20-year maturity bond with par value of $1000 makes semi-annual coupon payments at a coupon rate of 8%. Find the bond equivalent and effective annual yield to maturity of the bond if the price is $1000. Show all your computations.
5. (8 points) A 2-year bond with par value $1000 making annual coupon payments of $100 is priced at $1000. What will be the realized compound yield to maturity if the 1-year interest rate next year turns out to be 8%?
6. (25 points) Answer any five of the following questions:
- What is the Consumption CAPM?
- What is the difference between a theory based on the assumption that arbitrage opportunities cannot exist (such as the APT) and a theory based on risk-return dominance arguments that individual investors have private trade-offs between risk and return (such as the CAPM)?
- What can the concept of mental accounting help explain momentum in stock prices?
- What is survivorship bias and how might it affect tests of asset pricing models?
- There are sometimes reports of portfolio managers who seem to have done very well. Is this evidence that markets are not efficient?
- What is the put/call ratio and how is it used in technical analysis?
- What are TIPS? What does the yield-to-maturity on TIPS measure?
Solutions to Final
1.
- If academic studies indicate that stock prices are too low, then prices increase after the publication of these studies. This shows that investors pay attention to academic studies.
- They don't disappear entirely because it is costly to trade. If studies indicate that prices are too high, then it would be necessary to short-sell in order to profit from these anomalies; short selling can be costly, and further can be prohibited for some market participants, such as mutual funds. In general, when the price differential shrinks, there may no longer be potential for profits from exploiting these pricing differences.
- For arbitrage pricing theories, the reason is that given above -- trading is expensive. For asset pricing theories based on risk-return dominance, it is because there are many people who do not optimize their portfolios fully perhaps due to behavioral reasons or due to inertia, ignorance etc.
2.
- The forward 1-year interest rate is computed as (1.05)3/(1.045)2 - 1 = 0.0601 or 6.01%.
- The forward rate could decline if the market revised downward its expectations of inflation for year three, or if it revised downward expectations of the real rate of interest rate year. This latter case could be due to a softening of the business environment.
- The upward sloping curve could be due to expectations of higher future interest rates. Alternatively, it might simply reflect positive liquidity premiums because of an investor preference for shorter horizons.
- One would expect the yield curve to become flatter at higher maturities because the quality of information about the future tapers off. Our information regarding the economy 30 years from now is unlikely to be that different from our information regarding the economy 29 years from now.
3. Investors buy shares for cashflow rights and control rights, as well as because of pride in contributing to social welfare. In the case of social businesses, stock prices will decrease as return of capital is accomplished through dividends. However, they will not decline to zero because voters can still influence the way in which the money in the firm is invested. The price of a stock, therefore, will have two components. The first component will be the present value of future return-of-capital dividends; the second component will be the value of control. Since the value of assets-under-control is likely to increase over time, this component might very well increase over time. Hence we are likely to see stock prices of such companies decreasing first and then increasing over time. If control rights are not comparable over firms, then there may be several interrelated markets, as opposed to a single market for risk and return as models like the CAPM posit for standard dividend-paying stocks.
While it is possible that investors may bid up the price of the stock of a social business that is doing well on its social goals, this would simply transfer wealth from the purchasing investor to the selling investor; it would not provide any additional wealth to the firm itself. Hence the mechanism whereby the stock price would be affected in such a fashion is difficult to figure out.
4.
- If credit risk is expected to increase, then the price of a credit default swap will rise. Hence the most liquid method of exploiting this information is to buy a credit default swap (option i). The bond price would be expected to drop, so a short sale of the bond would also generate profits. However short sales involve arrangements with individual brokers and are not particularly liquid.
- If the quick ratio increases, the price would increase and the yield-to-maturity would decrease.
- The bond-equivalent yield to maturity would be 8% since the bond is selling at par. The effective annual yield to maturity is computed as (1.04)2-1 = 0.0816 or 8.16%.
5. The cashflows are $100 at the end of 1 year and $1100 at the end of the second year. The current price is $1000 since the bond is selling at par. If the yield drops to 8%, the $100 coupon will grow at 8% to become 100(1.08) or $108 at the end of year 2. Along with the face value payment of $1000 and the second period coupon of $100, the portfolio will have grown to 108+100+1000 = $1208 in two years, which amounts to an annualized rate of return of (1.28)0.5-1 = 0.0991 or 9.91%.
6.
- The consumption CAPM is an asset pricing model that assumes investors maximize the utility of consuming over multiple periods, instead of assuming that they maximize wealth at the end of one period. In this model, the measure of risk is the covariance of asset return with the growth rate of aggregate consumption. Practically, this means that in addition to the standard market beta, investors also take into account the ability of an asset to provide a hedge for changes in the future investment environment (e.g. providing an investment hedge).
- In the APT, the pricing relationship can hold for many assets, even if some investors do not hold their optimal portfolios, wherever the CAPM requires that all investors hold their optimal portfolios. Similarly, if pricing relationships go out of whack, attempts by some investors to capitalize on arbitrage opportunities will restore the pricing relationship. On the other hand, if the CAPM equilibrium doesn't hold, all investors will have to restructure their portfolios in order for the CAPM relationship to be re-established.
- Mental accounting is a sort of framing mechanism, whereby investors think of some cashflows differently from other cashflows. For example, if a stock goes up in price, the unrealized capital gains is treated differently than the initial value of the stock. The investor is likely to be more risk averse regarding the original capital than regarding the capital gain. Hence the investor is likely to be willing to take more risk, since a reduction is stock value is not considered serious, as long as capital gains are still positive -- even if they might drop from previous levels. This willingness to take more risk when prices are increasing leads to price momentum.
- Survivorship bias has to do with the fact that tests of asset pricing often only include stocks of companies that have not gone bankrupt. As a result, the computed average return is higher than would have been the case for an actual investor, since all the negative returns on stocks of bankrupt companies are left out. This means that estimated risk premiums are higher than they actually are.
- Not necessarily. First of all, some portfolio managers have to do better than average in order to make markets efficient, i.e. in order to make prices reflect all available information; these would be managers that are good at exploiting deviations from market efficiency. Secondly, after the fact, some managers will always appear to have done well, while others will appear to have done badly; this is independent of their actual skills and has to do with the fact that actual returns are unpredictable. However, there should be no correlation between the "outperforming" managers in one period and the "outperforming" managers in the next.
- The put/call ratio is the ratio of the open interest in puts (outstanding number of puts) of a stock to the open interest in calls of a stock. This ratio usually hovers around 65%. An increase in this ratio is supposed to be a leading indicator of a downward market correction. However contrarians believe that this is an indicator of a market rebound.
- TIPS stand for Treasury Inflation-Protected Securities. The face value of a TIPS security is increased to the extent of the rate of inflation. In a normal treasury security, if inflation increases, the real yield-to-maturity drops; however with a TIPS, there is some protection because of this increase in the face value. Hence the real rate of return is relatively constant. The yield on a TIPS measures the real rate of return plus the actual rate of inflation.
|
|