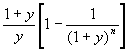 ;
this gives us (1.06/.06)[1-(1.06)-2] = 1.9433.
;
this gives us (1.06/.06)[1-(1.06)-2] = 1.9433. LUBIN
SCHOOL OF BUSINESS
Pace University
Fin 652 Investment Analysis
Fall 2000
Prof. P.V. Viswanath
Q. 1. Read the article below from the Wall Street Journal of December 18, 2000 and answer the following questions:
NEW YORK -- Treasurys rose Monday as the market awaits Tuesday's meeting of Federal Reserve officials, with many hoping the central bank will announce an aggressive response to the slowing U.S. economy.
In afternoon trading in New York, the 10-year note was up 10/32, or $3.125 per $1,000 face value at 104 19/32. Its yield, which moves inversely to its price, fell to 5.131% from 5.172% late Friday.
The 30-year bond rose 9/32 to 112 14/32, yielding 5.401%, down from 5.418% late Friday. The two-year note gained 4/32 to 100 20/32, yielding 5.276%.
Monday's gains, though modest, extended a sharp advance over the past two weeks. The yield on the benchmark 10-year note has dropped to 5.13% from 5.53% on Dec. 4.
2. (20 points) Suppose investors' horizons are the same and equal to 1 year. Then, the CAPM would imply E(Ri) - Rf = bi [E(Rm) - Rf], where Ri is the rate of return on any asset i, Rm is the rate of return on the market portfolio, bi is the market beta of asset i, and Rf is the rate of return on a 1 year T-bill. Use the definition of the liquidity premium (remember there are two different ways of expressing the liquidity premium), and the relationship between the beta of a bond and its duration to answer the following question:
3. Here is some information on Treasury bills from the Wall Street Journal Interactive edition. The following information is also available on the website:
Treasury bond, note and bill quotes are from midafternoon. Colons in bond and note bid-and-asked quotes represent 32nds; 101:01 means 101 1/32. Net change in 32nds. Treasury bill quotes in hundredths, quoted in terms of a discount rate. Days to maturity calculated from settlement date. All yields are to maturity and based on the asked quote.
| Maturity | Days to Mat. | Bid | Asked | Chg | Ask Yield |
|---|---|---|---|---|---|
| Dec 28 '00 | 9 | 5.35 | 5.27 | -0.12 | 5.35 |
| Jan 04 '01 | 16 | 5.60 | 5.52 | -0.08 | 5.61 |
| Jan 11 '01 | 23 | 5.65 | 5.57 | -0.08 | 5.67 |
1. a, b. The duration of a bond can be estimated as the negative of the ratio of the percentage price change to the percentage gross yield change, i.e. D = -(DP/P)/[Dy/(1+y)]. Applying this formula to the case of the 30 year bond and the 10 year bond, we have the durations as shown in the table below. Note that prices have been converted from thirty-seconds to decimals.
| New price | change | old price | new yield | change | old yield | Duration | |
| 30 yr bond | 112.4375 | 0.28125 | 112.1563 | 5.131 | -0.041 | 5.172 | 6.432582 |
| 10 yr note | 104.59375 | 0.3125 | 104.2813 | 5.401 | -0.017 | 5.418 | 18.58274 |
c. Assuming a coupon of 6%, and a price of par (of course, we have the true
original price, which is 100 20/32 - 4/32, or 100.5, but we use a price of $100
for convenience), the duration can be computed using the formula 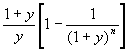 ;
this gives us (1.06/.06)[1-(1.06)-2] = 1.9433.
;
this gives us (1.06/.06)[1-(1.06)-2] = 1.9433.
We can now use the duration formula above to come up with the equation 1.9433 = - (4/32)/[(0.05276-x)/1+x], where x is the old yield (as of Friday close). Solving, we find x = 5.34342.
d. We first start by assuming a trial value for the coupon. This can be used to estimate a duration, which is then used to estimate the old yield (as in the c. above). Once the old yield is available, it can, once again, be used to compute a duration, using the formula in the first part of c. By iterating on this procedure, it should be possible to reach a point, where the duration computed changes very little from iteration to iteration (assuming the procedure converges).
2. According to the CAPM, E(Rlong-bond) = R1 yr. bond + Bond Beta(Market Risk Premium). We also know from the definition of the liquidity premium that E(Rlong-bond) - R1 yr. bond = Liquidity Premium. Hence Liquidity Premium = Bond Beta(Market Risk Premium). However, we also know that the bond beta = -br,m(Duration), where br,m is the sensitivity of interest rates to changes in the return on the market. Since all interest rates move in parallel, there is only one such beta. Putting the two equations together, we have -br,m(Duration)(Market Risk Premium) = Liquidity Premium. Now, since the Market Risk Premium and the br,m are the same for all bonds, while the duration of each bond is different, it is clear that hte liquidity premium must also differ from bond to bond.
3. a. The ask prices can be computed from the definition of the bond
equivalent yield, i.e. ![]() .
Plugging in rBEY =
0.0535, n = 9, and FV = 100, we can solve for the price of the first bill.
Following this approach, we compute the numbers given in the table below, in the
second-to-last column.
.
Plugging in rBEY =
0.0535, n = 9, and FV = 100, we can solve for the price of the first bill.
Following this approach, we compute the numbers given in the table below, in the
second-to-last column.
b. The forward yields are computed by simply taking the ratio of the prices of the relevant bonds. For example, the 1 week forward yield nine days ahead is computed by taking the ratio of 99.8683 to 99.7547, which yields 1.001138. We then deduct 1 from this, and multiply it by 365/7 to annualize it. This gives us the forward yield of 5.9365%. This is repeated for the second forward yield as well. The answers are given in the last column.
| Maturity | Days to Mat. | Bid | Asked | Chg | Ask Yield | Ask Price | Forw yld |
| Dec 28 '00 | 9 | 5.35 | 5.27 | -0.12 | 5.35 | 99.8683 | |
| Jan 04 '01 | 16 | 5.6 | 5.52 | -0.08 | 5.61 | 99.7547 | 0.059365 |
| Jan 11 '01 | 23 | 5.65 | 5.57 | -0.08 | 5.67 | 99.6440 | 0.057929 |
c. Since the forward rate is equal to the expected future spot rate plus the liquidity premium, we see that the expected future spot rate equals 5.7929 - 0.1 = 5.6929%.
d. Since this forecast is taken from the observed term structure, it is not possible to obtain abnormal profits from it (unless the investor has a better estimate of the liquidity premium). However, it is possible for an intending borrower to use it to choose between borrowing now and borrowing later (assuming the value of borrowing is the same for this person between now and then).