Risk and Return
©Prof. P.V. Viswanath, 1997, 2000

How to discount cashflows

Clearly, some cash flows are riskier than others. Equally clearly, riskier cashflows are worth less than less risky cash flows. In order, therefore, to value risky cash flows, we need to know two things:

Risky cash flows are, perforce, future cash flows. We know that we can value a future cash flow by discounting it at a given rate. Similarly, we can value risky future cash flows by discounting it at a higher rate than future riskless cash flows. The question, then, is: how much higher should a risky discount rate be than the corresponding riskless rate? Or, said differently, what is the risk premium per unit risk?  But first, we need to explore the nature or risk, itself.

Risk, essentially, has to do with uncertainty. The riskiness of an asset has to do with the uncertainty regarding the quantity of future cash flows that it will generate. Although we will be interested in measuring the riskiness of individual assets, primarily we care about the riskiness of the entire portfolio of assets that we possess, i.e our entire wealth. We will see, in short order, that our focus on asset portfolios will affect our definition of the riskiness of individual assets.

Given our ultimate concern, we first define the riskiness of a portfolio. This is defined as the variance of returns on the portfolio. The variance of returns is the average squared deviation from the mean return. One justification for using this measure of risk is that historically, portfolios with higher return variances have yielded higher average returns. variance of returns have, in the past, yielded higher returns.  

Portfolio Variance as a Measure of Portfolio Risk

The average return level is usually described by the expected value of the return and the risk is usually described by the variance of the return. The role of the expected return is clear: it gives us an idea of how high, the return is likely to be, on average. But how does variance measure risk?

Since the variance measures the spread of the distribution, we can learn something about the extent of uncertainty that exists regarding the return on the investment by looking at the variance. So variance measures risk in the sense of uncertainty.

However, some people intuitively associate risk with undesirable outcomes alone. If we think of the mean return as a "neutral" outcome, returns less than the mean would be "bad" outcomes and returns more than the mean would be "good" outcomes. If the return distribution is symmetric, this also means that good outcomes are as likely as bad outcomes. Since the variance measures the spread of the distribution around the mean, in this case, it would also give us a measure of how "bad" a bad outcome is likely to be, on average. However, if the distribution is not symmetric, then this is not true, and we need other measures such as skewness (the extent to which the distribution is skewed or tilted in one direction, instead of being symmetric) to give us this information. For symmetric distributions, like the normal distribution, the variance is a good measure of risk in this sense as well.

In what follows, we will interpret the concept of risk to mean uncertainty. However, the notion of variance as a measure of risk works only for portfolios containing the entire wealth of an individual --it does not work for the individual assets that make up the portfolio.

Risk Of Individual Assets Vs. The Risk Of Portfolios

The variance of returns can be used as a measure of risk if we are evaluating the entire portfolio of investments that an investor has.  However, if the investment under consideration is meant to be an addition to an existing portfolio, then the variance of the asset return is not appropriate as a measure of risk of this investment.  This is because we are interested primarily in the risk of our entire portfolio, and as far as this new asset is concerned, we would be interested in the incremental risk of the investment. The appropriate measure of the incremental risk of an investment differs from the variance, which is a measure of the total risk of the investment.

Consequently, we need to investigate how the variance of a portfolio is affected by the addition of a single asset.  First, we need to define a portfolio in a more formal manner, and see how its variance is related to the variances of the assets that make up the portfolio.

Portfolios Defined

A set of assets is called a portfolio.  If there are N assets in the economy, then we can define a portfolio by an N-vector containing the proportion of wealth invested in each of those N assets.  Hence, if a particular portfolio consists of $500 invested in asset 4 and $500 invested in asset 2, the portfolio will be defined by the set of N numbers:  (w1, w2, w3, w4,...., wn) = (0, 0.5, 0, 0.5, 0, 0,.....,0), i.e. wi is the proportion of the investment in the entire portfolio that is put in the ith asset.

The return on a portfolio is related to the returns on the individual assets by the formula 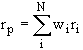, and hence, we have 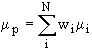, where ri is the return on the ith asset, and mi is the expected return on the ith asset.  However, the expression for the variance, denoted by s2, is more complicated, and is given by the following expression, where the subscript p refers to the portfolio, and sij refers to the covariance of returns between the ith and jth assets.

where the subscripts i , j in the second summation sign indicate that the sum is to be taken over all pairwise combinations of assets.

This expression can be visualized more easily in the following arrangement.

Asset 1 2 3 ... N
1  
2  
3  
.          
N  

The portfolio variance is obtained by adding up all the elements in this matrix.

Consider the following example of a portfolio consisting of investments in three stocks--Genentech, IBM, and Datatron.

  portfolio weights (wi) std deviations correlation coefficients
      Genentech IBM Datatron
Genentech 0.5 0.2 1 0.3 0.2
IBM 0.2 0.7 0.3 1 0.5
Datatron 0.3 0.05 0.2 0.5 1

Keeping in mind that the correlation coefficient r satisifies ri,j = si,j/(sisj), we can fill in the cells as above:

Stocks Genentech IBM Datatron
Genentech 0.01 0.0042 0.0003
IBM 0.0042 0.0196 0.00105
Datatron 0.0003 0.00105 0.000225

Adding up the elements in the cell, we get = 0.04093.

The Measure of Riskiness of a Single Asset

We are now ready to consider the marginal impact of an asset on the variance of a portfolio.  Consider the formula for the variance of a portfolio:

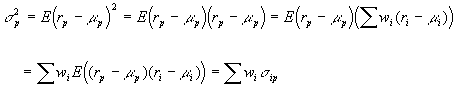
This formulation makes it obvious that asset i contributes to the risk of the portfolio (i.e. the variance of portfolio returns) at the rate of sip, i.e the covariance of returns between asset i and portfolio p.

The importance of covariances can also be appreciated by reconsidering the formula for portfolio variance. Note that there are N2 cells in all, with N variances, and N2-N covariances. For the special case, where all portfolio weights wi are equal to 1/N, all variances are equal to the average variance, , and all covariances are equal to the average covariance , we can write:

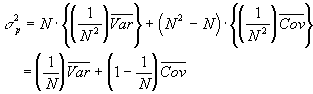
As the number of securities in the portfolio, the importance of the variance term decreases to zero, while that of the covariance term increases.

Risk Borne and Risk Compensated

The result that the risk of an individual asset in a portfolio is measured by the covariance of its returns with the portfolio returns is a useful one. However, according to this analysis, the measure of riskiness of a given asset is specific to the individual; hence this risk measure could differ from one person to another.

On the other hand, the market will not necessarily compensate each individual to the extent of the risk that s/he happens to bear on a given asset. As we saw before, it is possible to reduce portfolio variance through diversification. The market will be willing to compensate investors only for the risk that must be borne. We have to take equilibrium considerations into account to determine the nature of the asset risk that the market will actually compensate.

If we consider the economy as a whole, all the assets in the market must be held. Hence the market as a whole must bear the total risk, i.e. the variance of the return on the portfolio of all assets in the economy, which we term the market portfolio. The appropriate measure of risk of an individual asset, then, is the marginal contribution of that asset to the variance of the market portfolio.

Since we have already derived that the marginal contribution of an asset to the variance of a portfolio is the covariance of the return on that asset with the return on the portfolio, we see that im = Cov(Ri, Rm) measures the riskiness of an individual asset. The risk measure that is used in practice is this covariance normalized by the total variance of the market portfolio, which works fine if we are interested in the risk of an asset, relative to other assets. This measure is denoted by the greek letter beta and is written:

The Risk-Return Tradeoff for Individual Securities

Now that we have derived a common risk measure for all investors, we can specify the equilibrium risk-return tradeoff in the market.

The expected return on an asset can be divided into two parts: i) the return for deferring consumption, and ii) a compensation for bearing risk. The return for deferring compensation is, of course, simply rf, the return on the risk-free asset. Hence the return for bearing risk is E(ri) - rf. Mean-variance analysis implies that the return for bearing risk is proportional to the risk. Consequently, we can write the risk-return relationship as:

E(ri) - rf = bi [E(rm) - rf],

where the constant of proportionality is naturally the risk premium on the market portfolio, which has a beta of unity.

This equilibrium relationship has several desirable features:

The expected return on a security with a beta of zero is equal to the riskfree rate, rf. Since such a security contributes nothing to the (market) portfolio risk, it is effectively riskless (even though its return variance may be positive).

An asset with a beta of one is equivalent to the market portfolio and earns the expected rate of return on the market portfolio.

If two assets are priced to satisfy the above risk-return pricing equation, then so will their combination.

Portfolio Diversification

The risk of an asset, if held alone, is given by its variance. However, as we add other assets to the investor's portfolio, the variance decreases, in general, until it reaches a minimum level, which depends upon the covariances of the asset returns with each other. This is seen in the following figure, where the portfolio variance is depicted as a function of the number of securities in the portfolio, where the securities are chosen randomly for inclusion in the portfolio. The curve shown in the figure is actually an average of the different curves that might result in a large number of such simulations. Note that the portfolio variance decreases steadily until it reaches an asymptotic level. (Excel file with example)

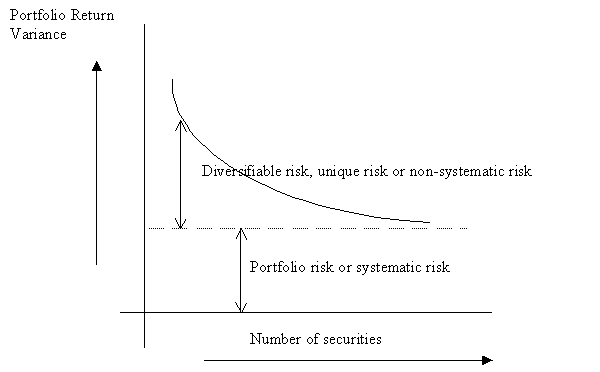
Figure: Behavior of portfolio return variance, as we increase the number of securities in a portfolio.

If we consider that the average investor holds the market portfolio, we can use the above picture to obtain another perspective on why the beta of an asset is the correct measure of its risk.  Asset-specific risk, or firm-specific risk is risk that is due to shocks that mainly affect the particular asset, while for our average investor, systematic risk is market-wide risk, which affects all assets in the economy to a greater or less degree. The main thing about asset-specific risks is that in large portfolios, such as the market portfolio, they offset each other. This phenomenon is called diversification. Hence, the only kind of risk that a holder of a large portfolio like the market portfolio needs to worry about is market-wide risk. It follows then, that the riskiness of an asset is simply the degree to which it is affected by market-wide risk.

Now, the risk compensation, or the additional average return that an investor obtains by holding the market portfolio rather than a riskless portfolio is E(Rm)-Rf, where E(Rm) is the average or mean return on the market portfolio, and Rf is the return on a riskfree asset. Suppose the return on a given asset changes by a multiple b of the change in the market return, i.e. that b is the sensitivity of the asset to the changes in the market return. It is, then, reasonable to define the riskiness of the asset as being equal to b times the riskiness of the market portfolio. Consequently, the additional average return that the holder of such an asset can expect is b times the risk compensation on the market portfolio. In other words, for an arbitrary asset, i,

E(Ri) = Rf + bi[E(Rm) - Rf]

which is precisely the relation that we derived earlier.  This risk-return relationship is called the CAPM equation, short for Capital Asset Pricing Equation.  (From this, we note another interpretation of b in addition to the mathematical definition given above, viz.bi = im/Var(Rm).

A security or asset beta is similar to a covariance. Thus, it measures the degree to which a security's returns comove with the returns on the market. Because of the standardization, the beta can be interpreted as the slope of the regression line of the security or asset return on the market return. This regression line is also called a characteristic line.

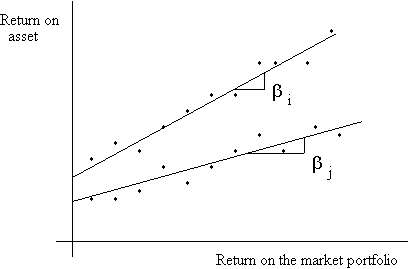
Asset i, in the picture above, has a larger beta than asset j.

Betas have the additional useful properties:

; the beta of a portfolio is the weighted average of the assets that make up the portfolio.

; the market beta equals one.

What happens if market prices deviate from equilibrium?

Consider the following graph showing the equilibrium relationship between expected return and beta risk under the CAPM (also called the security market line):

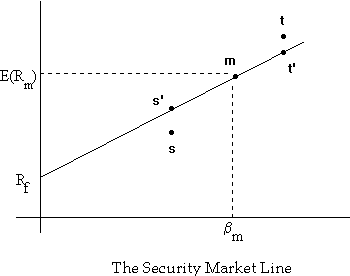
Security s has an expected returns less than that implied by its beta and is overpriced, while security t has an expected return greater than that implied by its beta and is underpriced. Under these circumstances, nobody would hold security s, preferring to hold the synthetic security s' constructed by taking a combination of the riskfree asset and the market portfolio. This would cause the price of security s to drop until its expected return equalled that of security s', and hence on the security market line.

Q: How would security t's price return to its correct level?

Applications of the CAPM to Capital Budgeting

Barriott Hotels Inc. is considering the acquisition of an existing hotel, 'Quality of Life' near Newark airport. Barriott's M&A team has looked over the books of Quality and has concluded that if Barriott were to acquire Quality, it could expect an annual cash flow, net of maintenance expenditures, of $200m. for the first year, with future cash flows growing at a rate of 4%. It has been estimated that Quality's cash flows are somewhat more variable than that of the market and, hence, that they have a beta of about 1.2. If the return on the market portfolio is expected to be 15% per annum, and one year T-bills yield 6% currently, what is the maximum price that Barriott should be willing to pay for Quality?

The discount rate for Quality's cash flows is the rate of return that would be required by the market for an asset with cash flows of similar risk. This is given by

Rf + bQual [E(Rm)-Rf] = 0.06 + 1.2 (0.15 - 0.06) = 0.168.

Discounting the expected cash flows at this rate, we find that the PV of Quality's cash flows are 200/(.168-.04) = $1562.5 m.

Determination of the Appropriate Discount Rate when the New Project is a Scaled Down Version of the Firm

If the new project is a scaled down version of the entire firm, then the beta of the new project is the same as the beta of the firm's assets. This is the same as the beta of the firm's liabilities, given the equality of asset and liability values under double-entry bookkeeping.

If there is only equity in the firm's capital structure, then the beta of the firm's stock is equal to the beta of such a project. If there is debt and equity in the firm's capital structure, then the firm's liabilities can be considered a portfolio of the debt and the equity, and we can compute the project beta from the result that the beta of a portfolio's returns is equal to the weighted average of the betas of the assets comprising the portfolio.

which leads to the result that the required return on such a project is:

If interest payments are tax deductible for the corporation, then the effective cost of debt capital is actually (1-t)E(RDebt), where E(RDebt) is the average market rate of return earned by investors on the debt.

The Arbitrage Pricing Model

Now, let us spruce up the CAPM a little bit. Suppose market-wide risk is not a homogenous entity. Suppose some assets share some aspects of this market- wide risk, while other assets share other aspects of this market-wide risk. These different aspects are called factors. The formula for the expected return on an asset, then, becomes:

E(Ri) = Rf + b1i[E(Rm1) - Rf] + b2i[E(Rm2) - Rf] + ... + bni[E(Rmn) - Rf]

where E(Rmj) is the average return on the jth factor, and b2i is the sensitivity of the ith asset to the 2nd factor, and so on.

Go to FIN320 Home Page

Go to Prof. P.V. Viswanath's Home Page