Portfolio Performance Evaluation
© P.V. Viswanath, 1998

Measuring Investment Returns:

The concept of measuring investment returns is more complicated if we are dealing with returns over several periods.

Time-weighted versus Dollar-weighted returns:

Dollar weighted returns depend upon the sequence of inflows and outflows of cash into the portfolio. If this sequence is within the control of the portfolio manager, then dollar weighting is appropriate; else, time-weighting is preferable.

Thus, if a portfolio manager invested $50 at time zero, and $51 at time one, and ended up with a portfolio value of $112 at time two, how would we evaluate the manager of this fund?

Using the Dollar-weighted return method, which is essentially to compute the internal rate of return, we solve the following equation for r.

.

Solving, we find r = 7.117%

But this performance may not all be due to the manager's handiwork. Consider the following, call it alternative 1. Suppose the manager, himself, is investing in an index. Suppose the value of an index share at time 0 is $50. Then the manager would be able to buy 1 index share. Suppose the index level goes up to 51 at time 1. Then the manager buys another index share. At time 2, the index level is 56, providing a portfolio value of $112 as in the example above. However, this is not the only way the numbers in our simple example could have come about.

Consider alternative 2. Suppose the value of an index share at time 0 is $50, as before. At time 1, the index value drops to 40. The manager now buys 51/40 = 1.275 units. The index value goes up to 49.23 leaving a portfolio value of $112 as before.

Under alternative 3, the value of an index share is $50 at time 0; at time 1, it goes up to $65. The manager buys 0.7846 index shares with it. At time 2, the index value goes down to $62.76 leaving a portfolio value of $112 as before.

In all three alternatives, the dollar weighted return is 7.117%. Now, if the manager had no control over the flows, the three scenarios are not equivalent. The manager's contribution is the selection of the index as the investment vehicle. Let's look at the return over the two periods on the index. In alternative 1, it's (56/50)0.5-1 or 5.83%. In alternative 2, it's (49.23/50)0.5-1 or -0.77%%. In alternative 3, it's (62.76/50)0.5-1 or -12.04%.

This second method of computing the return is called time-weighting. Time-weighting could be done in two ways, by using the arithmetic average or the geometric average.

Arithmetic averages versus geometric averages: Geometric averages are a good estimate of past performance, while arithmetic averages are a good measure of future performance. This is true, because the arithmetic average is an unbiased estimate of the portfolio’s expected future return. The geometric return is always less than the arithmetic average, and hence, a downward biased estimate of the portfolio’s expected future return.

The Conventional Theory of Performance Evaluation:

Comparing across funds.

Sharpe’s measure: (rp-rf)/sp

This measures the reward to total volatility trade-off. This is appropriate when the objective is to measure the performance of overall portfolios that contain the entire wealth of the investor. This follows easily if investors maximize mean-variance utility functions. Note, furthermore, that SP = rSM + aP/sP, where r is the correlation coefficient between the portfolio being evaluated and the market portfolio.  This shows that a portfolio's Sharpe measure can be improved by picking high alpha stocks.

Treynor’s measure: (rp-rf)/bp

This measure gives the average return per unit of systematic risk. This is appropriate when we are comparing several portfolios that are all going to be part of a larger overall portfolio. Note that .

Jensen’s measure: ap= rp-rf +bp(rm-rf)]

This is the portfolio’s alpha value. This is a version of the Treynor measure, that is appropriate if leverage is not feasible. In general, it is dominated by the Treynor measure.

Appraisal ratio: ap/s(ep)

This measures abnormal return per unit of diversifiable risk. This measure is appropriate to evaluate an active portfolio that is going to be combined with a larger, passive, diversified portfolio. Thisis because the following relationship exists between the Sharpe measure for the composite portfolio and that for the benchmark market portfolio:

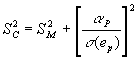
We already know that the appropriate evaluation measure for the composite portfolio assuming a mean-variance utility function is the Sharpe measure. In this case, the Sharpe measure for the market portfolio obviously is not within the control of the portfolio manager. Hence the second component, which is the square of the appraisal ratio is the appropriate evaluation measure.

 

Potential bias in these measures:

Performance Attribution Procedures: (See text).

Components of Investment Performance:

 

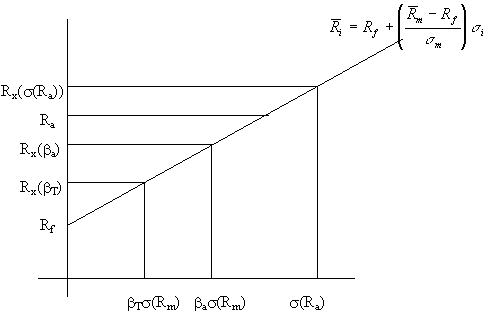
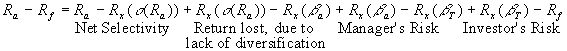
Ra is the actual performance. Rx(.) is the risk-adjusted return for a portfolio consisting of the market portfolio and the riskfree asset, with the prescribed characteristic.

Rx(.) refers to the ex-post return. In other words, in a bull market, we would have average portfolio return positively related to portfolio beta as in the above picture. In a bear market, higher beta stocks would exaggerate market movements, and hence would have lower average returns. In the scenario shown in the above graph, the market turned out to be a bull market, and the manager was vindicated in his choice of a higher beta. However, if it had been a bear market, the Manager's risk component would have been negative.

If the portfolio chosen by the manager is the same as the market portfolio, then ba s (Rm) would be equal to s(Ra). Else, bas (Rm) < s(Ra). Consequently, a portfolio constructed by combining the market portfolio with the riskfree asset to generate a portfolio standard deviation equal to s(Ra) would need to have a beta higher than ba. Therefore, the 'Return lost due to lack of diversification' component would be positive in a bull market, and negative in a bear market. Net selectivity would be positive in a bull market only if the manager could choose a portfolio good enough to overcome the lost diversification due to the decreased diversification. In the above picture, net selectivity is negative.

Market Timing:

Run a regression of the excess portfolio return on two independent variables, one being simply the excess market return, and the other equal to the product of the excess market return and a dummy variable equal to 1 in bull markets and 0 in bear markets. Then the sum of the coefficients is equal to the beta in bull markets and the coefficient of the first variable alone is equal to the beta in bear markets.

Other links 

Go to Fin 652 Home Page
Go to Prof. P.V. Viswanath's Home Page