Valuing Bonds

© P.V. Viswanath

A bond is a security with a fixed cash flow per period, C, and a balloon payment, F, at the end of the bond's life. The periodic $C cash flow is called a coupon, and the single $F payment is called the bond's face value. The bond's life is called the bond maturity, and the coupon payment is usually made every six months. The ratio of the total coupon payments per year (2C in this case) to the face value is called the coupon rate. (Note that this coupon rate is not an interest rate, and does not reflect a loan market price.) In return for these promised payments, the purchaser of the bond pays a price, which depends on the bond characteristics. We can use the formulas generated earlier to price different kinds of bonds, once we know the appropriate interest rate.

Pure Discount Bonds

A pure discount bond, or a zero-coupon bond has a coupon rate of 0%. Any compensation to the bondholder comes solely from the difference between the bond's purchase price and the face value of the bond.

If a bond has a face value of $F, and a maturity of T years, and the appropriate (effective annual) discount rate for a given bond is r%, the bond's price is given by:

Price = PV =

Example: If F = $100,000; T = 8 years; and the annual discount rate is 9%, the bond should sell for = $50,186.63

Level Coupon Bonds:

Such a bond has a coupon rate that does not vary over the life of the bond. This can be priced as a combination of an annuity and a pure discount bond.

If a bond has a face value of $F, and a maturity of T years, a coupon rate of c% (where C = cF/100 is the total interest paid each year), and the appropriate (effective annual) discount rate for a given bond is r%, the bond's cash flows are given by:

Let r0.5 be the effective six-monthly rate defined by (1+r0.5)2 = 1+r. Then, the price is given by:

Price = PV = F/(1+r)T + (C/2) x (Annuity factor with interest rate = r0.5 and number of periods = 2T). 

Example:

If F = $100,000; T = 8 years; the coupon rate is 10%, and the annual discount rate is 9%, the six-monthly rate is 4.4%, and the bond's price is: 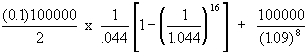= $106,765.94.  Note that if the six-monthly discount rate is 4.4%, with coupons being paid semi-annually as in the current case, it is customary to say that the bond sells at a yield of 2 times 4.4% or 8.8%.  This is similar to the concept of APR or annualized percentage rate.

Consols

A consol has an infinite maturity, and is priced simply as [C/2]/r0.5, where we are assuming that the coupon is paid every six months, and r0.5 is the discount rate for 6 months, i.e. 2r0.5 is the annual yield on the consol.

Example:

If C = $10,000, and the annualized discount rate is 9%, the price is $113,557.26.

Bond Pricing with Non-Flat Term structure of Interest Rates

In principle, as we noted above, there is no reason to assume that the the price in any given period, of a dollar to be paid in the following period, is the same. In other words, ri, the i-period interest rate can vary by i.

For example, if r3 = 9%, a three-year pure discount bond with a face value of $1000 will sell for 1000/(1.09)3 = 772.18. If r2 = 11%, a two-year pure discount bond with a face value of $1000 will sell for 1000/(1.11)2 = 811.62

If ri is the same for all i, we say that the term structure is flat. Else if ri is a rising (falling) function of i, we say that the term structure is rising (falling).

A bond with annual coupon payments of $100 and a maturity of 3 years with a face value of $1000 would be priced as follows:

If r1=0.1, r2 = 0.11, and r3 = 0.09, the price is $1,021.47.

Yield To Maturity

Suppose a 3 year, 8% coupon rate, $1000 face value bond is selling for $949.22. What is the rate of return on this bond for a purchaser? If the term structure is flat, the rate of return is simply equal to the prevailing interest rate. If the term structure does not change over the life of the bond, this rate of return is independent of the bond's holding period. However, if the term structure is not flat, the rate of return will depend upon the holding period, as we saw above.

However, we can impute a unique rate of return called the yield to maturity. This is the single discount rate that will set the present value of the bond purchase to zero. Assuming that the coupon payments are semi-annual, the six-monthly yield to maturity is computed by solving:

(This is a kind of a weighted average of the 6-month rate, and the appropriate forward rates.)

Solving for r in this equation (by trial and error) gives us r = 0.05. This is used to compute the bond yield, defined as twice the computed six-monthly yield-to-maturity, which works out to 10%. If the term structure is flat, the yield-to-maturity also corresponds to a market interest rate. The bond yield, therefore is like an APR or a stated rate. In this case, the effective annual market interest rate is (1.05)2 -1 or 10.25%. However, it is common to refer to the bond's (annual) yield-to-maturity as 10%.

The Relation Between Bond Yield And Coupon Rate

Suppose the six-monthly market rate of interest is 4.4%; i.e. the bond yield is 8.8%, and the effective annual rate of interest is 9% for bonds of all maturities.

Consider the following three bonds:

Bond 1: A 2 year, 10% coupon bond with a $1000 face value.

Bond 2: A 2 year, 8.8% coupon bond with a $1000 face value.

Bond 3: A 2 year, 8% coupon bond with a $1000 face value.

Note that the bonds only vary by coupon rate. The prices of the bonds are equal to 50 + 1000/(1.09)2 = 50 x 3.596 + 841.68 = 1021.46

44 + 1000/(1.09)2 = 44 x 3.596 + 841.68 = 1000.00

40 + 1000/(1.09)2 = 40 x 3.596 + 841.68 = 985.51

Note that the present value of the bond is equal to the face value if the six-monthly coupon rate is equal to the six-monthly effective rate of interest. Such a bond is said to be price at par. If the coupon rate is below the rate of interest, the bond is said to sell at a discount. If the coupon rate is above the rate of interest, the bond is said to sell at a premium.

The Relation Between Bond Yield And Bond Price

Again, consider the bond 1, the 2 year, 10% coupon bond with a $1000 face value. If we continue to suppose that the bond yield is 8.8%, the price is 1021.46.

Now suppose the market bond yield drops to 7.8%. The market price is now given by 50 + 1000/(1.039)4 = 1040.02.

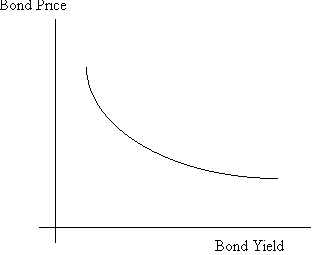
In fact, as the bond yield drops, the bond price rises, and vice-versa.

Tax Treatment of Bonds:

§The price appreciation on original issue discount (OID) bonds is an implicit interest payment.  Hence the IRS calculates a price appreciation and imputes taxable interest income.  Additional gains or losses due to market yield changes are treated as capital gains.

§Example: An 8% 30 yr. bond issued at 81.071% of par is sold for 820.95 at the end of the year.  If interest income is taxed at 36% and capital gains at 28%, the tax paid equals 0.36(80 + 811.80 - 810.71) + 0.28(820.95-811.80) = $31.75.
(YTM at issue = 10%; yearend price using this YTM = 811.80)

Practical Bond Pricing:

There are several ways of pricing a bond ex ante:

Construct a yield curve from the observed prices of bonds that are selling in the market; interpolate the yield of a bond with the same maturity as the bond to be valued; price the bond using the discounted cash flow pricing equation, using the yield to maturity as the discount rate for cash flows of all maturities. (This method may not give the right answer if the bond is not actually priced close to par).

Construct a yield curve as above; infer the term structure of interest rates; price the bond using the discounted cash flow pricing equation, using the appropriate discount rate for each cash flow

Use an asset-pricing theory (such as the CAPM or the APT) to deduce the required rates of return and then use the discounted cash flow pricing equation.

Forward Rates:

Suppose we have a non-flat term structure of interest rates. Then, the rate of interest on a 1-period loan starting one year from now is not necessarily equal to r1. This interest rate, call it f, is called a forward rate (because it is for a future period. (Similarly, we can define other one-year and multi-year forward rates for other time periods.)

Suppose that the term structure does not change over time. Then, $1 invested today will be worth 1+r1 in 1 year. If this is invested for one more year, the value of the investment grows at the forward rate, f, which is the interest rate for that period. Hence the value of the investment in 2 years is (1+r1)(1+f). But the investment value after 2 years must also be (1+r2)2 , because this is simply a 2-year investment. 2-year loan. From this, we see that (1+r2)2 = (1+r1)(1+f), or . Note that the two-year rate is simply a geometric average of the one year rate and the one-year forward rate beginning one year from now. Similarly, the 3-year rate is the geometric average of the 1-year rate, the 1-year forward rate on a loan beginning one year from now, and the 1-year forward rate on a loan beginning two years from now. From the formula above, we can also write: f = .

The return on an investment over a given period is defined as . Hence the return over the first year is . The return over the second year is . That is, the rate of return over the second period is equal to the forward rate for that period. (Note: If interest rates change over time, then the holding period rate of return can be different from the forward rate for the same period.)