Webster's dictionary defines science as "the observation, identification, description, experimental investigation, and theoretical explanation of a class of phenomena." Why do we want to explain, to understand? Because we can use this understanding to predict what will happen to quantities of interest under a carefully specified set of circumstances if we undertake certain actions. Understanding the theory of finance is a prerequisite to good financial decision-making. Rules of thumb are limited in their scope. They can take you only so far. At some point, you must think! A rule of thumb can only be used to solve problems that are familiar. In other words, a rule of thumb is good for solving problems that are not really problems.
Because of the fact that a corporation operates in a competitive environment, rules of thumb and following the herd can never lead to superior performance. At best, performance will be average, and at worst, performance will be hurt because of inappropriate use of conventional rules.
A model is a method of depicting reality, or better said, it is a method of abstracting the essentials of reality. Of course, what is essential depends on the questions being investigated; hence every model will be different even though the reality may be the same.
Consider the last question. We agreed, earlier, that the correct objective of the manager was to maximize the stock price, or more generally to maximize the value of the firm. But how can he use this broad goal to arrive at the right decision in a particular situation?
Suppose our manager is faced with the situation described in the following case of Danforth and Donnalley Laundry Products Company. What decision should be taken?
On April 14, 1983, at 3:00 P.M., James Danforth, president of Danforth & Donnalley (D&D) Laundry Products Company, called to order a meeting of the financial directors. The purpose of the meeting was to make a capital budgeting decision with respect to the introduction and production of a new product, a liquid detergent called Blast.
...(see textbook for rest of case)
We see that the answer to the original question that we posed is none too clear, at first blush. What decision should Danforth take? How is he to take into account the detailed cash flow analyses that have been prepared by Rainey? What about the marketing implications of the new product introduction? How important is market share retention? What about corporate strategy? If shareholder wealth is important, how is Danforth to know what his shareholders want? Should he send out a questionnaire?
Clearly, some framework is needed in order to allow Danforth to come to a decision. Before dealing with the particulars of the Danforth and Donnalley case, let us consider a more abstract situation:
(The suggested solution to the Danforth and Donnalley case can be seen by clicking here. It is recommended that you work through the rest of this chapter, and preferably, the first part of the next chapter on Some Alternative Investment Rules before looking at the solution.)
Let us assume
In setting up this framework (model), we recognize production as the raison d'etre of the firm. The allowance for two periods takes into account the lag between investment and (uncertain) production of consumer goods.
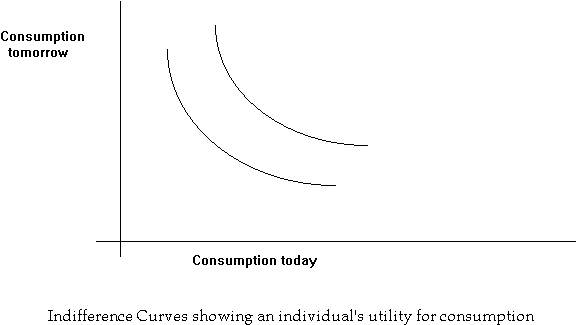
We model a consumer using the technique of indifference curves:
An individual is better off, the greater the possible consumption in each period.
An individual can improve his utility through production, i.e real investment. Production involves reducing consumption today by a certain amount, and using it for transformation into a greater number of units tomorrow.
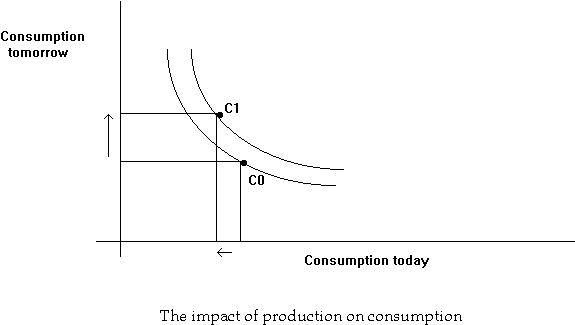
A consumer's utility can also be improved by trading in the market for loans:
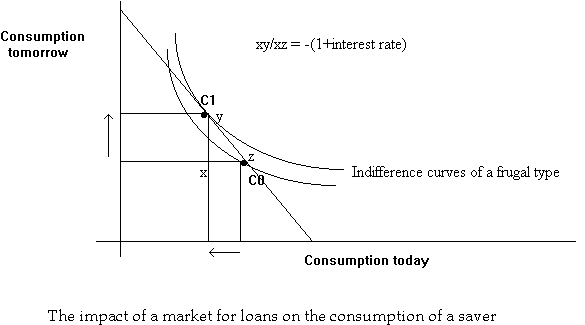
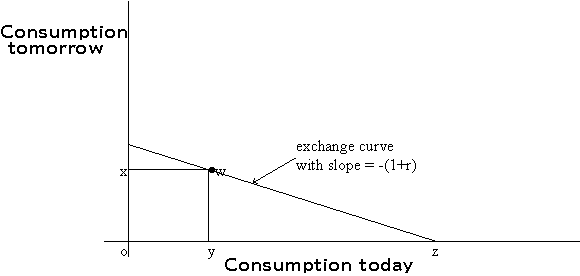
The market for loans involves the exchange of consumption goods today for consumption goods tomorrow and vice-versa. Suppose we can trade at the rate of yx units of tomorrow's consumption units for xz units of today's consumption units.
Starting at the point C0, we could consume on any other point on the line joining C0 and C1, depending upon how many units were exchanged. The following are examples of feasible trades:
| Today | Tomorrow |
| xz | xy |
| 0.5 xz | 0.5 xy |
| 1 | xy/xz |
| 1 |  |
| 1 | 1+r |
| 1/(1+r) | 1 |
The price, in tomorrow's consumption units, of a unit of consumption to be obtained today, is given by the negative of the slope of this exchange curve.
From the table above, r is the number of additional units of tomorrow's consumption units can be obtained by giving up 1 unit today. We call r, the interest rate; the slope of the exchange curve is -(1+r), which is equal to yx/xz.
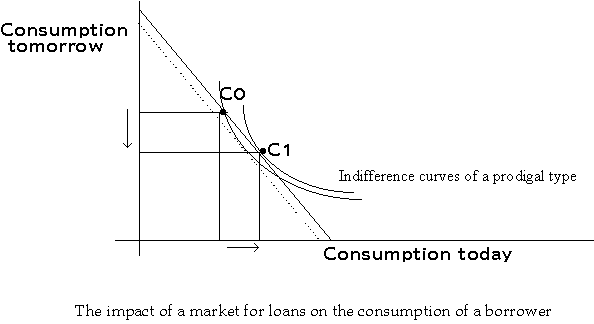
Once a market for loans is possible, consumption plans can be altered by trading in this market. A prodigal consumer (spender) can use the market to transfer consumption from tomorrow to today at the market rate. Note that through such a transfer, the prodigal reaches a higher exchange curve, and hence, a higher indifference curve.
Similarly, a frugal consumer (saver) can use the market to transfer consumption from today to tomorrow at the market rate.
Now let us consider a manager of a corporation presented with a particular investment/production project that moves the shareholders from a consumption plan C0 to a consumption plan C1. Is this a desirable project?
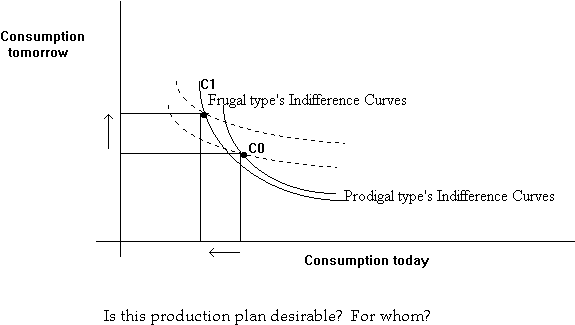
We see that if the shareholders are similar to the frugal individual, this is a desirable investment; but not so if they resemble the prodigal. In the absence of a market, two individuals can disagree on the desirability of a certain production plan/project. Hence there is no unambiguous index of firm value.
The prescribed action for a manager is not clear in such a situation. It would seem that he would need to check his stockholders' preferences before taking any action at all! This is not a desirable state of affairs: if you remember, the strength of a corporation lies in the ability to separate ownership from management. How can this problem be resolved?
The answer is that if a market for loans exists, all individuals whether they be frugal or prodigal will agree unambiguously on the desirability of a given project. This is because the existence of the market determines an equilibrium price in today's dollars for future resources. This allows a manager in a corporation, where ownership is separated from management, and where the owners (shareholders) may differ from day to day, to act according to a well-defined criterion.
This unambiguous criterion is that of Net Present Value, which is defined as the difference between the present value of the new consumption plan less the present value of the old consumption plan, evaluated at the market rate of interest. If the NPV is positive, the value of the firm goes up by that amount, and hence the manager should accept the project.
Let us now see how the manager can act according to this criterion, and how it achieves the manager's goal of stockholder wealth maximization.
Consider the present value of an arbitrary consumption plan (oy units today, ox units tomorrow):
PV(consumption plan) = PV(oy today, ox tomorrow)
= PV(oy today) + PV(ox tomorrow)
= oy + ox (today's value of 1 unit of tomorrow's consumption)
= 
= oy + ox (yz/wy) = oy + yz = oz.
In other words, the present value of a consumption plan is simply the x-intercept of the exchange curve passing through the consumption point.
Now let us compare two production plans:
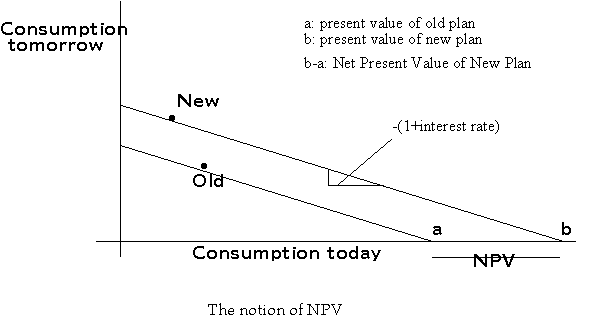
The new plan is on a higher exchange curve, and it has a higher present value. The Incremental or Net Present Value (NPV) of the move from the old plan to the new plan, i.e. the project under consideration is, then, equal to (b-a).
We have seen how the NPV of a project can be computed graphically. We will now see how to compute the NPV of a project mathematically.
Note that the NPV is not affected by changing the point of reference. Hence we can arbitrarily define the old consumption plan as zero, and define the new consumption plan with reference to the old consumption plan.
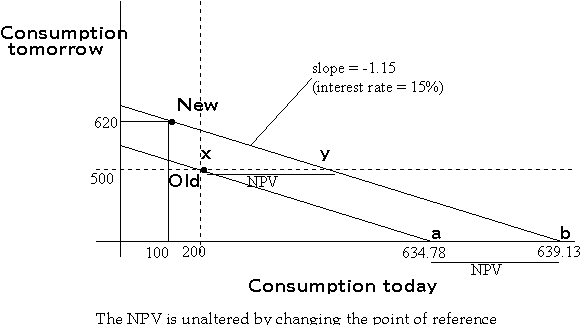
In the scenario presented above, the move from the old plan to the new plan (i.e. the project) calls for decreasing current consumption by $100 (investing $100) with a resulting increase in consumption tomorrow by $120 (payoff tomorrow from the project), and the market rate of interest for transferring consumption between today and tomorrow is 15%.
Proj. NPV = -PV(200 today; 500 tomorrow) + PV(100 today; 620 tomorrow)
= Present Value of (-100 today, 120 tomorrow)
= 
= $4.35.
Hence, the (present) value of the firm will increase by $4.35 if the project is undertaken.
How can we be sure that both the frugal and the prodigal types will agree on this conclusion?
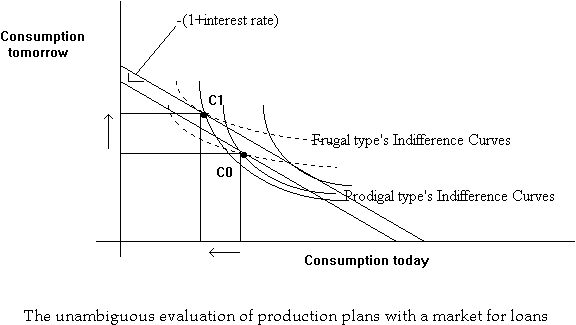
We see that they will both agree because undertaking the new project brings both of them to a higher exchange curve, which means that they will both be on higher indifference curves.
If a given shareholder does not agree with a particular dividend pattern implied by the investment policies of the manager, he/she can always borrow/lend to suit his/her own consumption preferences. Furthermore, if there is a market for the shares of the corporation, then the individual can sell his/her shares and buy into the stock of another company that has a more desirable investment policy (from the point of view of this investor).
When does the NPV rule not work? If there are transactions costs, it may not always be easy for an investor to just cash out his/her ownership of a particular company that has a different pattern of dividend payments. Under these circumstances, we may expect clienteles, i.e. similar individuals choosing to hold shares in the same firm. For example, there may be dividend clienteles--different firms that follow different dividend policies. If there are clienteles, then the manager will use a decision rule that is optimal for his shareholder clientele--a rule that may differ from a simple Maximize NPV rule.
Another case is if borrowing rates are different from lending rates:
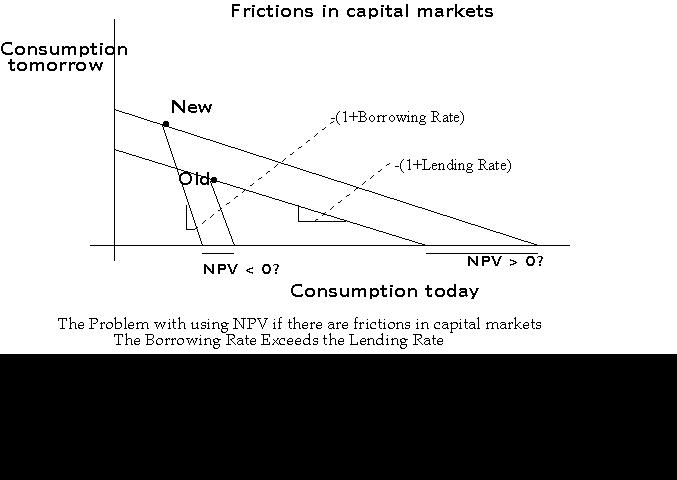In this
case, once again, clienteles may develop, with one set of
corporations using higher required rates of return (and paying
higher dividend rates), and another set of corporations (growth
firms) using lower required rates of return and paying lower
dividend yields.
We have seen that the present value (PV) of a two-period project-- a project with a cash flow of -C0 today and C1 tomorrow is -C0 + C1/1+r, where 1/(1+r) is the price today for $1 to be paid tomorrow. How do we evaluate projects with cash flows in more than two periods?
Let us denote a project by a vector of its cash flows. A project requiring an investment today of $100 with cash flows of $10 next year, $20 the following year, and $150 the year after that would be denoted (-100, 10, 20, 150).
Strictly speaking, to evaluate such a project, we would need to know the price today of $1 to be paid one year from now, the price today of $1 to be paid the year after that, and the price today of $1 to be paid in the year following that. In other words, we would need to know the one-year, two-year and three-year interest rates. These rates need not all be the same. The pattern of interest rates is called the term structure, and is shown below.
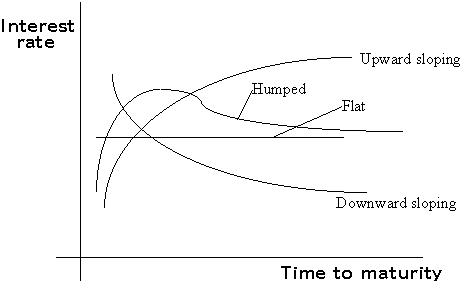
For convenience, let us make the following assumption:
The price in any period, of $1 to be paid in the following period, is the same.
This corresponds to the flat term structure in the graph above. This means that the interest rate is constant for all maturities. If we denote this common interest rate as r, the common price in any period of $1 to be paid in the following period is 1/(1+r). I.e., the price at time t of $1 to be paid at t+1 is equal to 1/(1+r), and so is the price at time t+1 of $1 to be paid at t+2 equal to 1/(1+r).
Now, consider the price at time t (today) of a $1 to be paid at time t+2 (in two years). The value of this at t+1 must be 1/(1+r), since the payment date (t+2) then would be just one year away. Hence, getting $1 two years from today is equally as valuable as getting 1/(1+r) one year from now. But getting 1/(1+r) one year from now is worth [1/(1+r)] [1/(1+r)] or simply 1/(1+r)2.
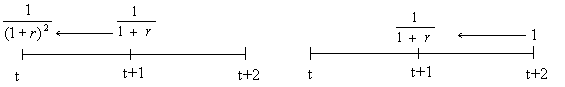
This is called compounding. This can be easily generalized to show that:
PV ($1 to be paid in n years) = 
. And correspondingly,
Future Value, in n years ($1) = (1+r)n.
Letting r = 12%, we can evaluate our project:
PV(project) = -100 + 10 (1/1.12) + 20 (1/1.12)2 + 150 (1/1.12)3 = 28.25
Earlier on, we defined the interest rate, r, for a period as the number of additional dollars that could be obtained in the loan market at the end of the period in return for giving up $1 today. Correspondingly, if the interest rate for one year is r%, the The present value or, price today, of $1 to be paid in one year is 1/1+r.
If we assume that the term structure is flat, can we determine the interest rate for 6 months?
Let us denote this 6-monthly interest rate by r0.5. If we now treat six months as one period, we can use our earlier formula to conclude that the price today of $1 to be paid after 2 six-monthly periods is 1/(1+r0.5)2. But, since two six-monthly periods are equal to one year, we already know that this price is 1/1+r. Hence:
1/1+r = 1/(1+r0.5)2. Or, r0.5 = sq. root(1+r) - 1 = (1+r)0.5 - 1. Generalizing, we find:
rm = (1+r)m - 1.
If we turn this formula around, we have: r = (1+rm)1/m - 1. I.e., if rm is the periodic interest rate, then the annual (per year) interest rate is (1+rm)1/m - 1.
In other words, to annualize an interest rate, i, that applies to a period less than a year, we compute (1+i)k -1, where k ( the reciprocal of the period length, in years) is the number of these periods in a year. If this computed rate equals s, then an investment of $1 in the loan market today yields $1+i after 1 period, and $1+s after 1 year.
A popular way of turning a periodic interest rate into an annual rate is by multiplying the periodic rate by the number of periods in a year. This is called the APR. However, this is not a true interest rate.
If i is the interest rate for 1 period (less than a year), then APR = i k, where k is the number of these periods in a year. However, an investment of $1 in the loan market today will not yield $1+APR after 1 year. Rather, it will yield (1+i)k -1 as computed before.
Example: Suppose you have taken out a loan to buy your car,
with monthly payments, and you are being charged interest at a stated
rate (APR) of 24%. The actual monthly interest rate is 24/12 =
2%. Hence, if the purchase price is $10,000 and the money must be
paid in three equal monthly instalments of $C each, the present
value of the monthly payments must equal $10,000. In other words,
.
To distinguish between this type of annualization from the previous type of annualization, we refer to the former as an effective interest rate. The effective annual rate, in this case, would be (1.02)12 - 1 = 0.2682 or 26.82%.
Consequently, if we wanted to pay off the entire amount in a single payment at the end of 1 year, we would have to pay, not 10000 (1.24) = $12400, but rather 10000 (1.2682) = $12,682.
If the stated rate is r%, and compounding will be done
k times a year, then after n years, an initial investment of $C
will grow to 
. If compounding is continuous, that
investment will grow to Cern.
In general, the PV of a project with cash flows (-C0, C1, C2, ..., Cn) is:
,
where r is the appropriate effective interest rate per period.
If the periodic cash flows are equal and extend out to
perpetuity, i.e. the project is (0, C, C, ..., C, ...), then the
above formula can be simplified to 
. For example, if C = $20, and r = 5%,
the present value = 20/.05 = $400. Correspondingly, if $400 are
invested at 5% p.a., there would be an interest flow of $20 per
year forever.
Suppose the cash flows are growing at the rate of g% per period, i.e. the project is (0, C, C(1+g), C(1+g)2, ..., C(1+g)n-1, ...),
then 
If the periodic cash flows are equal, but they stop after a finite time, say n periods, i.e. the project is ((0, C, C, ..., C),
then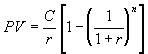 
.
The term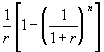 
is denoted 
and is called the annuity
factor. We can then write: PV (annuity) = C 
.
Note that an n-year annuity is the same as a perpetuity less
another perpetuity with payments delayed for n years. Hence PV
(n-year annuity) = PV(perpetuity) - PV(perpetuity)/(1+r)n
Suppose the cash flows are growing at the rate of g% per period, and they end after n periods. i.e. the project is (0, C, C(1+g), C(1+g)2, ..., C(1+g)n-1),
then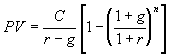 
Problem 4.29, Ross and Westerfield:
In January 1984, Richard Gossage signed a contract that guaranteed him a minimum of $9,955,000. The guaranteed payments were $875,000 for 1984, $650,000 for 1985, $800,000 for 1986, $1 m. in 1987, $1 m. in 1988 and $300,000 in 1989. In addition, the contract called for $5,330,000 in deferred money payable at the rate of $240,000 per year from 1990 through 20006 and then $125,000 a year from 2007 through 2016. If the relevant annual interest rate is 9% and all payments are made on July 1 of ecah year, what would the present value of these guaranteed payments be on January 1, 1984? If he were to receive an equal annual salary at the end of each of the 5 years from 1984 through 1988, what would his equivalent annual salary be?
Solution:
The cash flows are:
| 1984 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990- 2006 | 2007-2016 |
| 875,000 | 650,000 | 800,000 | 1,000,000 | 1,000,000 | 300,000 | 240,000 | 125,000 |
The value of the guaranteed contract is:
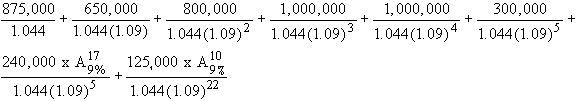which
works out to $5,051,150.
The equivalent five-year, annual salary is the annuity which solves:
$5,051,150 = C x 
, which yields C = $1,298,596.
Other Chapters:
Go to FIN
301 Home Page.
Go to P.V.
Viswanath's Home Page.