Regression Analysis
© P.V. Viswanath, 2002
Regression Analysis
In regression analysis, we start with the set of points that
we have in the graph above. We then posit a linear relation
between the variable on the y-axis (rTr) and the
variable on the x-axis (rMa), 
.
However, it is obvious that this relationship is not exact.
Hence, we add an additional term, called the residual that takes
account of this departure from linearity. Symbolically, we write:
.
We then choose values for the constants a and b, such that the
importance of the residual or error term, t, is minimized. To
find a unique set of values a and b, we impose, the restriction
that the sum of the squared residuals, 
,
be minimized, so that no individual residual becomes too large.
This defines a unique value for b, which is related to the
covariance:
.
We put a hat over the b, to indicate that this is an estimate of the true value of b in the linear relationship between rTr and rMa in the population.
The estimate of a is 
. Then, for any given value of rMa,
the predicted value of rTr is simply 
.
For our sample, this estimated relationship is shown in the
output from a spreadsheet regression command:
Constant = 0.0044271 X Coefficient(s) = 0.4557292
R Squared = 0.6995842 Std Err of Coef. = 0.1055852
The return on Trump stock, rTr, is the dependent variable, since we are predicting it, while rMa, the return on Marriott stock, is the independent variable. The Y-variable refers to the dependent variable, and the X-variable refers to the independent variable.
From this output, we see that the estimated regression equation is:
rTr = 0.004427 + 0.45573 rMa.
The standard error of the estimated coefficient, which is
0.1055852 indicates the degree of our confidence in the
coefficient estimate. Just as the given sample is just one of the
many samples that could have been generated by our posited
underlying relationship describing rTr and rMa,
i.e. 
, we
can also think of this regression as one of the many
corresponding regressions.
With this approach, the estimated coefficient for rMa is the estimated mean of the probability distribution of coefficients that such repeated regressions would generate. The standard error, 0.1056, is then like the estimated standard deviation of this probability distribution of coefficients.
This graph shows the actual relationship in the sample between rTr and rMa, and the estimated relationship:
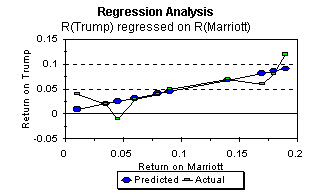
As we saw earlier in our discussion of linear functions, the
estimated intercept â is the predicted value of rTr
if rMa were zero. The estimated coefficient of rMa
in the regression equation, 
, is simply the slope of the estimated
linear relationship.
For each pair of values, rMa and rTr, in
the sample, we can compute the residual, which is equal to 
. In the graph,
this is simply the vertical distance between each actual value
and its predicted value.
Example:
2. Here are the results of a regression of the returns on Cisco Systems (CSCO) on the returns on a portfolio tracking the S&P 500, using data from February 1994 to December 1999:
|
Beta Regression for CSCO |
||||||
|
Regression Statistics |
||||||
|
Multiple R |
0.510354 |
|||||
|
R Square |
0.260461 |
|||||
|
Adjusted R Square |
0.249743 |
|||||
|
Standard Error |
0.093309 |
|||||
|
Observations |
71 |
|||||
|
ANOVA |
||||||
|
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
1 |
0.211581 |
0.211581 |
24.30136 |
5.45E-06 |
|
|
Residual |
69 |
0.600752 |
0.008707 |
|||
|
Total |
70 |
0.812332 |
|
|
|
|
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
0.027427 |
0.012218 |
2.244826 |
0.027988 |
0.003053 |
0.051801 |
|
RCSCO |
1.387554 |
0.281472 |
4.929641 |
5.45E-06 |
0.826034 |
1.949075 |
a. What is the estimated beta of CSCO? (5 points)
b. What percentage of the return on CSCO cannot be explained by movements in the S&P 500? (5 points)
c. Can you reject the hypothesis that the average return on CSCO can be explained by the CAPM over the sample period, taking into account the uncertainty in the system? Use the point estimate of the CSCO beta to answer this question. (10 points)
d. The beta estimation for CSCO over the sample period is given below:
|
Regression using April 1990 to Dec. 1993 |
||||||
|
Regression Statistics |
||||||
|
Multiple R |
0.447362 |
|||||
|
R Square |
0.200133 |
|||||
|
Adjusted R Square |
0.181531 |
|||||
|
Standard Error |
0.121373 |
|||||
|
Observations |
45 |
|||||
|
ANOVA |
||||||
|
|
df |
SS |
MS |
F |
Significance F |
|
|
Regression |
1 |
0.158494 |
0.158494 |
10.7589 |
0.002062 |
|
|
Residual |
43 |
0.633449 |
0.014731 |
|||
|
Total |
44 |
0.791943 |
|
|
|
|
|
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
|
Intercept |
0.062248 |
0.018806 |
3.309956 |
0.001895 |
0.024321 |
0.100174 |
|
RCSCO |
1.62435 |
0.495217 |
3.280077 |
0.002062 |
0.62565 |
2.623049 |
g. (Bonus question) Did the true beta risk of CSCO change from the 1990-1993 period to the 1994-99 period? Explain your answer. If you believe it did change, what in your opinion, caused the change? (5 points)
Solution:
2. a. The estimated beta can be read out from the Coefficients column as 1.387554, or approximately 1.39.
2. b. The R2 of a regression measures the proportion of the variance of the dependent variable that can be explained by the independent variable. Hence, in this case, the percentage of the return on CSCO that cannot be explained by movements in the S&P 500 is 1 - 0.260461 or approximately 74%.
2. c. The predicted value of the intercept, using the CAPM, and assuming that the estimated beta is correct is (1-1.3876)(0.004432) = -0.001718, which is outside the 95% confidence limits for the intercept. This suggests that the CAPM has underestimated the return on CSCO for the period.
2. d. It certainly looks like the beta changed; the point estimate went from 1.624 in the earlier period to 1.388 in the later period. However, the 1.624 number is within the 95% confidence interval for the later period beta; the 1.388 in the later period is also within the 95% confidence interval for the earlier period beta. This makes it more difficult to insist that the beta has decreased. Similarly, it would probably be difficult to claim that the operations of CSCO have changed from the first period to the second. On the other hand, CSCO was a new stock in the earlier period with an unproven technology; in the last five to ten years, it has matured somewhat, and it is conceivable that this has decreased the sensitivity of CSCO's stock price to market movements.