Capital Asset Pricing Model

© P.V. Viswanath, 2001

Assumptions of the CAPM:

• No transactions costs.
• Assets are infinitely divisible.
• No personal income taxes.
• Perfect competition--an individual cannot affect the price of a asset by his/her buying or selling.
• All assets, including human capital, are marketable.
• All investors have the same information.
• Investors make their decisions based solely on the expected returns and variances of portfolio returns.
• Unlimited short sales are allowed.
• Unlimited lending and borrowing is permitted at the riskless rate.

Under these assumptions, all investors have the same variance-covariance matrix, and every investor's efficient set will look the same. Hence, we have the following result.

The Separation Theorem:

The risky component of the optimal portfolio for any investor is the same portfolio, and is independent of the investor's risk preferences.

The risk measure of an asset under the CAPM

If every investor's risky portfolio is the same, this portfolio is simply the portfolio of all risky assets in the market. Hence this is called the market portfolio and depicted by the letter m.

A corollary of this is that the riskiness of any individual asset can be measured by _im, the covariance between the returns on asset i, and the returns on the market portfolio.

We standardize this measure by dividing by , the variance of returns on the market portfolio. This standardized measure is termed an asset's beta, and given by the formula: .

Asset Betas:

The characteristics of an asset beta are similar to that of a covariance. Thus, it measures the degree to which an asset's returns comove with the returns on the market. Because of the standardization, the beta can be interpreted as the slope of the regression line of the asset return on the market return. This regression line is also called a characteristic line.

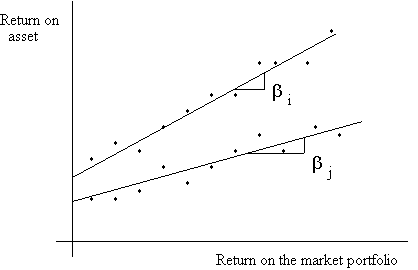
Asset i has a larger beta than asset j.

Click here for an Excel file with an example of how to compute asset betas.

Betas have the additional useful properties:

; the beta of a portfolio is the weighted average of the assets that make up the portfolio.

; the market beta equals one.

You can find more information on fundamental determinants of asset betas elsewhere in my webnotes.

The risk-return tradeoff for individual securities:

Now that we have derived a common risk measure for all investors, we can specify the equilibrium risk-return tradeoff in the market.

The expected return on an asset can be divided into two parts: i) the return for deferring consumption, and ii) a compensation for bearing risk. The return for deferring compensation is, of course, simply r_f, the return on the risk-free asset. Hence the return for bearing risk is E(r_i) - r_f. Mean-variance analysis implies that the return for bearing risk is proportional to the risk. Consequently, we can write the CAPM pricing relationship as:

E(r_i) - r_f = beta_i [E(r_m) - r_f],

where the constant of proportionality is naturally the risk premium on the market portfolio, which has a beta of unity.

This equilibrium relationship has several desirable features:

The expected return on a security with a beta of zero is equal to the riskfree rate, r_f. Since such a security contributes nothing to the (market) portfolio risk, it is effectively riskless (even though its return variance may be positive).

An asset with a beta of one is equivalent to the market portfolio and earns the expected rate of return on the market portfolio.

If two assets are priced to satisfy the CAPM pricing equation, then so will their combination.

The risk-return tradeoff for efficient portfolios:

The CAPM pricing equation gives us the required rates of return on individual assets and portfolios. This is seen in the linear relationship that we have just derived between expected returns and asset betas. This relationship is called the Security Market Line. (Click here for an Excel file showing the Security Market Line.) However, from the efficient frontier, we can derive another pricing equation for efficient portfolios:

.

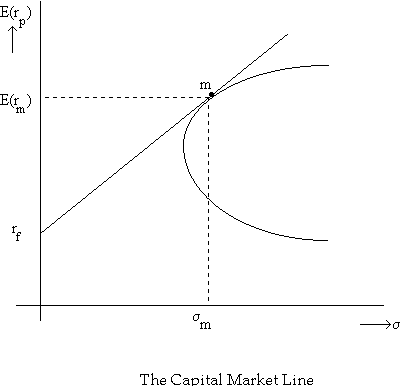
This corresponds to the efficient frontier (also called the capital market line) in the graph below, where m indicates the market portfolio. (Click here for an Excel file with a worked out example of an economy, showing the Capital Market Line that would result if the CAPM held.)

What happens if market prices deviate from equilibrium?

Consider the following graph showing the equilibrium relationship between expected return and beta risk under the CAPM (the security market line):

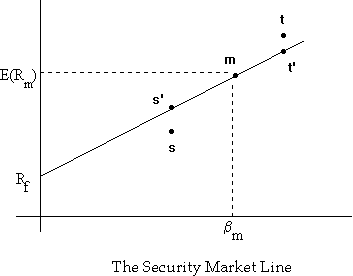
Security s has an expected returns less than that implied by its beta and is overpriced, while security t has an expected return greater than that implied by its beta and is underpriced. Under these circumstances, nobody would hold security s, preferring to hold the synthetic security s' constructed by taking a combination of the riskfree asset and the market portfolio. This would cause the price of security s to drop until its expected return equalled that of security s', and hence on the security market line.

Q: How would security t's price return to its correct level?

Applications of the CAPM to Capital Budgeting

Barriott Hotels Inc. is considering the acquisition of an existing hotel, 'Quality of Life' near Newark airport. Barriott's M&A team has looked over the books of Quality and has concluded that if Barriott were to acquire Quality, it could expect an annual cash flow, net of maintenance expenditures, of $200m. for the first year, with future cash flows growing at a rate of 4%. It has been estimated that Quality's cash flows are somewhat more variable than that of the market and, hence, that they have a beta of about 1.2. If the return on the market portfolio is expected to be 15% per annum, and one year T-bills yield 6% currently, what is the maximum price that Barriott should be willing to pay for Quality?

The discount rate for Quality's cash flows is the rate of return that would be required by the market for an asset with cash flows of similar risk. This is given by

R_f + Beta_Qual [E(R_m)-R_f] = 0.06 + 1.2 (0.15 - 0.06) = 0.168.

Discounting the expected cash flows at this rate, we find that the PV of Quality's cash flows are 200/(.168-.04) = $1562.5 m.

Determination of the appropriate discount rate when the new project is a scaled down version of the firm:

If the new project is a scaled down version of the entire firm, then the beta of the new project is the same as the beta of the firm's assets. This is the same as the beta of the firm's liabilities, given the equality of asset and liability values under double-entry bookkeeping.

If there is only equity in the firm's capital structure, then the beta of the firm's stock is equal to the beta of such a project. If there is debt and equity in the firm's capital structure, then the firm's liabilities can be considered a portfolio of the debt and the equity, and we can compute the project beta from the result that the beta of a portfolio's returns is equal to the weighted average of the betas of the assets comprising the portfolio.

which leads to the result that the required return on such a project is:

If interest payments are tax deductible for the corporation, then the effective cost of debt capital is actually (1-)E(R_Debt), where E(R_Debt) is the average market rate of return earned by investors on the debt.

Go to Prof. P.V. Viswanath's Home Page

Go to the FIN 301 Home Page
Go to the FIN 320 Home Page
Go to FIN 652 Home Page
Go to FIN 351 Home Page